関連記事
空間ベクトルの成分表示
平面ベクトルと同様、どの方向にどれくらいの大きさかを表す場合ベクトルの成分表示を使って表現することが出来る。空間ベクトルの場合、以下のように3つの成分を用いて表現する。
$$
\vec{a} = (3,1,2)
$$
このベクトルは以下の図のように $x$ 軸方向に3、$y$ 軸方向に1、$z$ 軸方向に2進めたベクトルである。
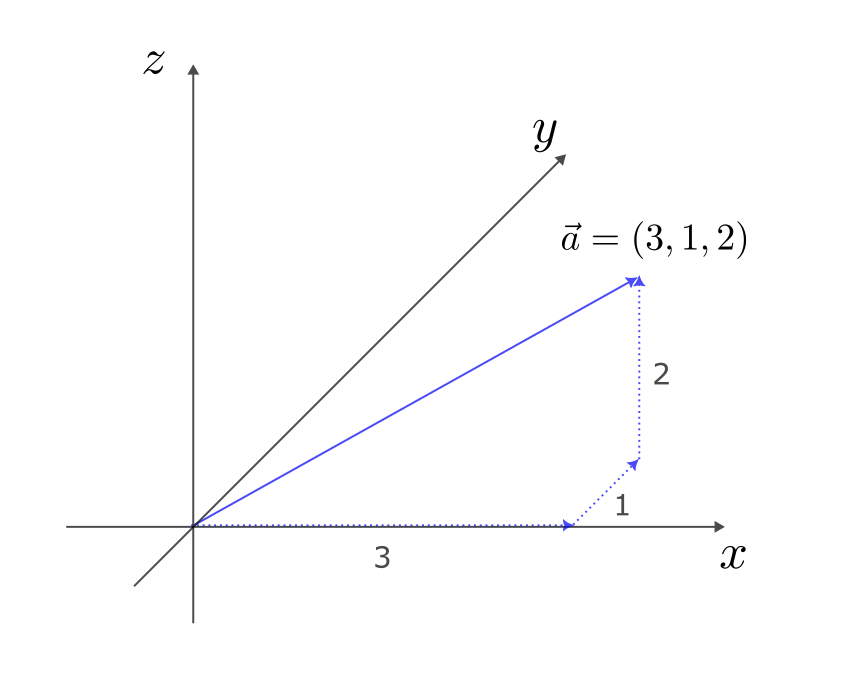
$\vec{a}$ の大きさは三平方の定理から
$$
|\vec{a}| = \sqrt{3^2 + 1^2 + 2^2} = \sqrt{14}
$$
となる。
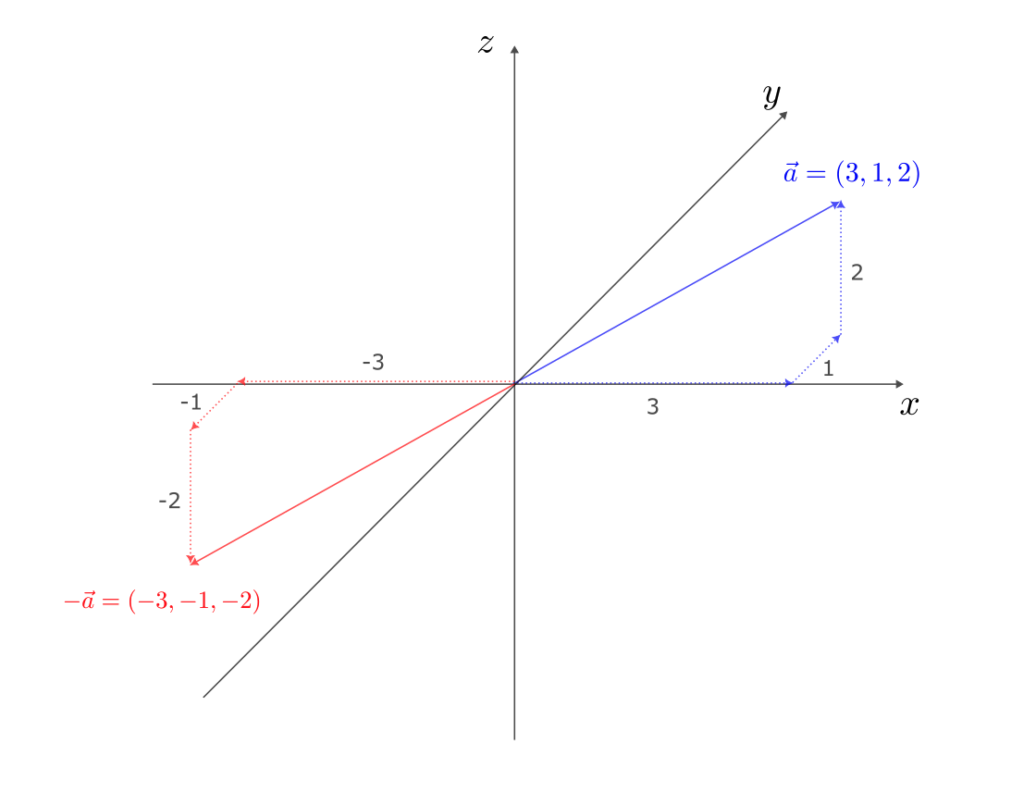
$\vec{a}$ の逆ベクトルは
$$
-\vec{a} = (-3,-1,-2)
$$
である。
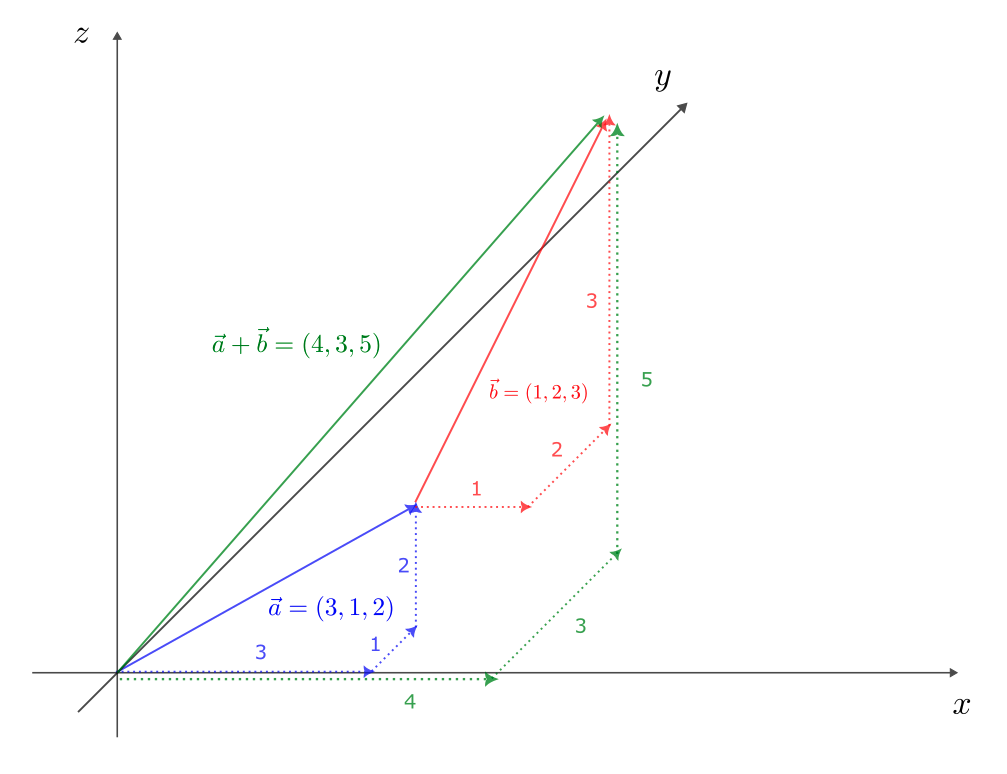
$\vec{b} = (1,2,3)$ とすると、
$$
\vec{a} + \vec{b} = (3 + 1,1 + 2,2 + 3) = (4,3,5)
$$
となる。
同一平面上にある3つのベクトル
以降、このページでは特に断りがない限り、2つ以上のベクトルを考える際、始点は同じ位置にあるものとする。
イメージ
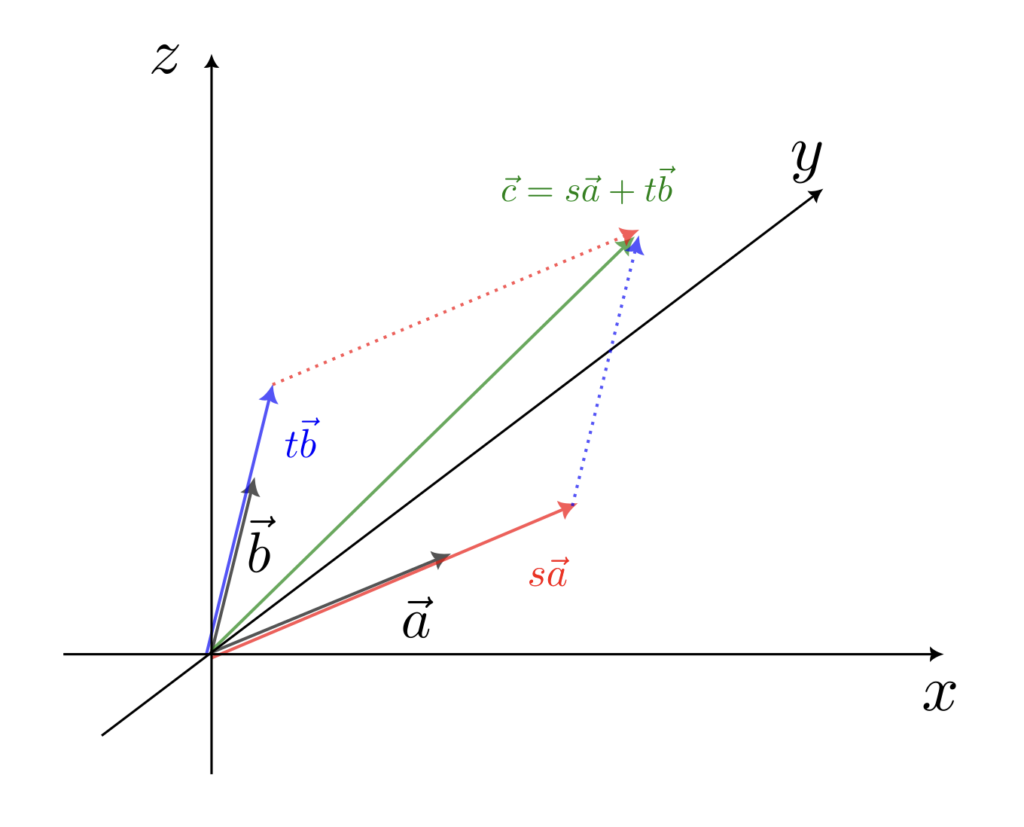
3つの空間上のベクトル $\vec{a}$ と $\vec{b}$ と $\vec{c}$ が同一平面上にあるとは、$\vec{c}$ は $\vec{a}$ のスカラー倍と $\vec{b}$ のスカラー倍の和で表せる、つまり
ある実数 $s, t$ に対して、
$$
\vec{c} = s\vec{a} + t\vec{b}
$$
と表せれることである。
例1
$$
\vec{a} = (3,1,2),\ \vec{b} = (2,4,6),\ \vec{c} = (4,3,5)
$$
とする。
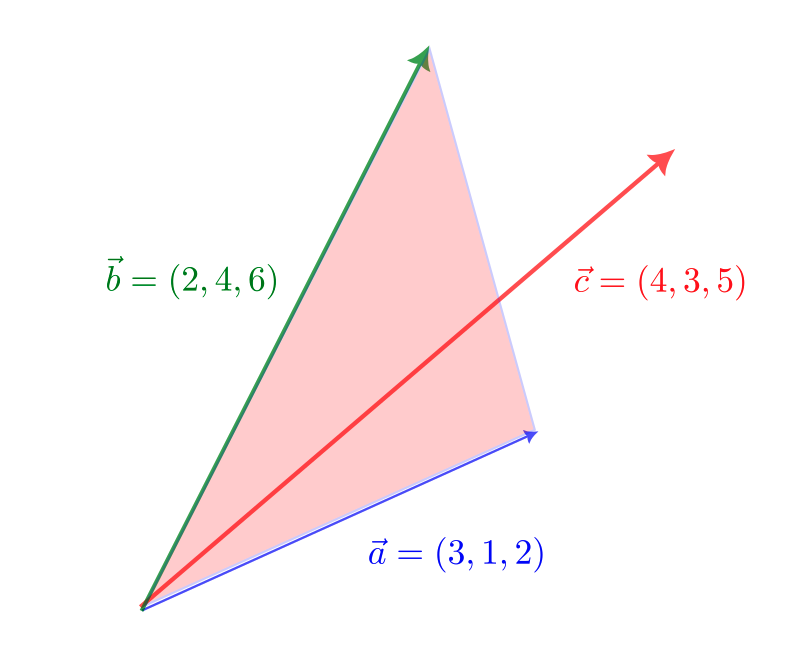
このとき、
$$
\begin{align}
\vec{c} &= (4,3,5) \\
&= (3,1,2) + \frac{1}{2}(2,4,6) \\
&= \vec{a} + \frac{1}{2}\vec{b}
\end{align}
$$
と表せるため、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にある。
例2
$$
\vec{a} = (3,1,2),\ \vec{b} = (2,2,2),\ \vec{c} = (1,2,3)
$$
とする。
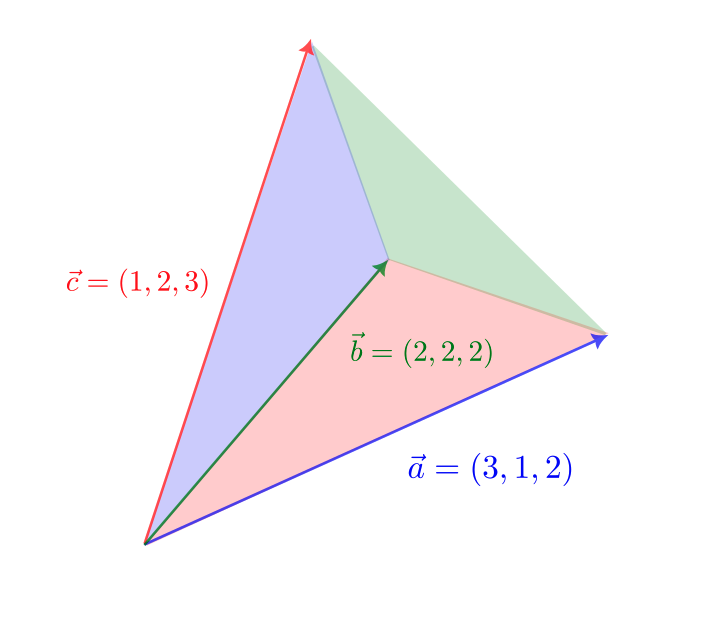
$\vec{c} = s\vec{a} + t\vec{b}$ とすると、
$$
s\vec{a} + t\vec{b} = (3s + 2t, s + 2t, 2s + 2t)
$$
より
$$
\begin{cases}
3s + 2t = 1 \\
s + 2l = 2 \\
2s + 2t = 3
\end{cases}
$$
となる。しかし、この方程式を満たす $s$ と $t$ は存在しない。
例えば、上の2式で連立方程式を解くと、$s = -\frac{1}{2}, t = \frac{5}{4}$ であるが、これは、$2s + 2t = 3$ の解ではない。
よって、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にない。


