関連記事
目標
この記事の目標は以下の定理を示すことである。
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立である $\Leftrightarrow$ 任意の空間ベクトル $\vec{p}$ に対して、
$$
\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}
$$
を満たす $s, t, u$ が唯一つ存在することは同値である。
例
空間ベクトル2で考えた例を扱う。
例1
$$
\vec{a} = (3,1,2),\ \vec{b} = (2,2,2),\ \vec{c} = (1,2,3)
$$
とする。
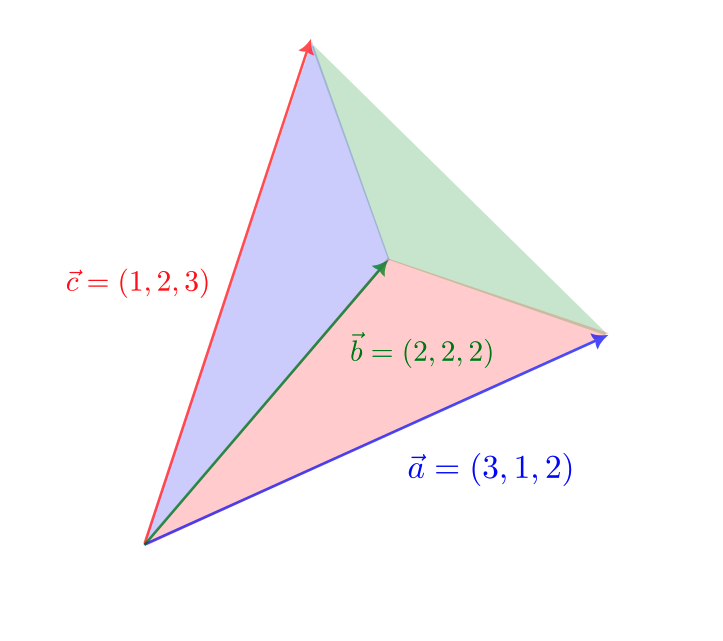
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立である。
$\vec{p} = (x, y, z)$, $\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}$ とすると、
$$
\begin{cases}
3s + 2t + u = x \\
s + 2t + 2u = y \\
2s + 2t + 3u = z
\end{cases}
$$
である。
$s,t,u$ についての連立方程式を解くと、
$$
s = \frac{x-2y+z}{3}, t = \frac{x + 7y -5z}{6}, u = \frac{-x-y+2z}{3}
$$
となり、これ以外の解は持たない。
よって、任意のベクトル $\vec{p} = (x,y,z)$ をとると、
$$
\vec{p} = \frac{x-2y+z}{3}\vec{a} + \frac{-x-y+2z}{3}\vec{b} + \frac{x+7y-5z}{3}\vec{c}
$$
と表すことができる。
例2
$$
\vec{a} = (3,1,2),\ \vec{b} = (2,4,6),\ \vec{c} = (4,3,5)
$$
とする。
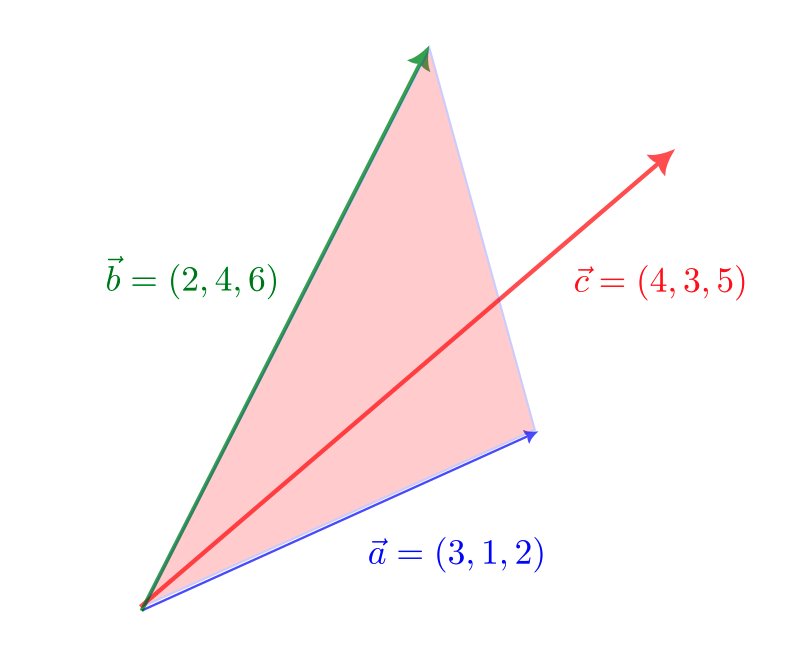
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にあり、1次独立ではない。
例えば、$\vec{p} = (0,0,1)$ とする。
このとき、$\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}$ の形で表せれるとすると、
$$
\begin{cases}
3s + 2t + 4u = 0\ \cdots\ ① \\
s + 4t + 3u = 0\ \cdots\ ② \\
2s + 6t + 5u =1\ \cdots\ ③
\end{cases}
$$
となる。
(② × 3) – ① をすると、$2t + u = 0$ となり、(② × 2) – ③ をすると、$2t + u = -1$ となる。
しかし、これを満たす $t,u$ は存在しないため、$\vec{p} = (0,0,1)$ は $\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}$ という形で表すことができない。
定理の証明の前に
定理の証明のポイントとなるところは、
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立である $\Rightarrow$ 任意のベクトル $\vec{p}$ に対して、
$$
\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}
$$
と表せる、というところである。
図で考えてみると、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立であることから、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にないため、$\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}$ で表せそうである事はイメージできる。
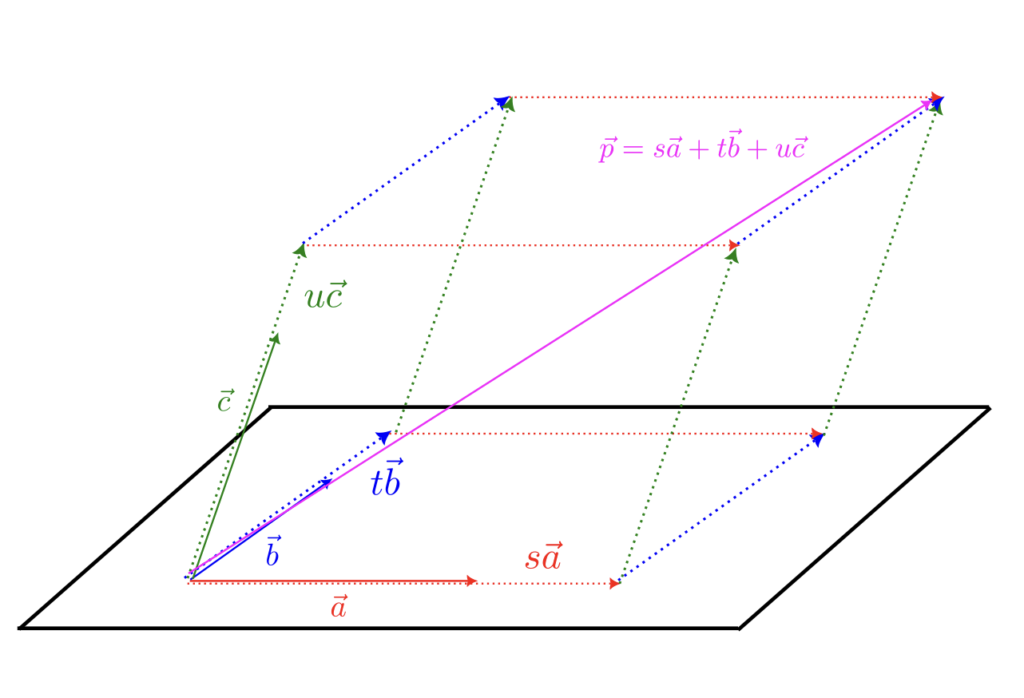
成分表示を利用して考えてみると、
$\vec{a} = (a_1,a_2,a_3),\vec{b} = (b_1,b_2,b_3),\vec{c} = (c_1,c_2,c_3)$ とする。
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立とすると、任意の $\vec{p} = (p_1, p_2, p_2)$ に対して、連立方程式
$$
\begin{cases}
a_1s + b_1t + c_1u = x \\
a_2s + b_2t + c_2u = y \\
a_3s + b_3t + c_3u = z
\end{cases}
$$
を満たす $s,t,u$ が存在するかを考える必要がある。
しかし、今回は連立方程式を利用して証明する方法ではなく、別の方法で証明することにする。
証明の方針としては、まず任意のベクトル $\vec{p}$ に対して、
$$
\vec{p} = s_0\vec{a’} + t_0\vec{b’} + u_0\vec{c’}
$$
で表せる1次独立なベクトル $\vec{a’}$ と $\vec{b’}$ と $\vec{c’}$ を見つける。
(実際、例1でやったようにそのようなベクトルは存在する。)
そこから、$\vec{a’}$ を $\vec{a}$ にしても、$\vec{p} = s_1\vec{a} + t_1\vec{b’} + u_2\vec{c’}$ の形で表せることを示す。
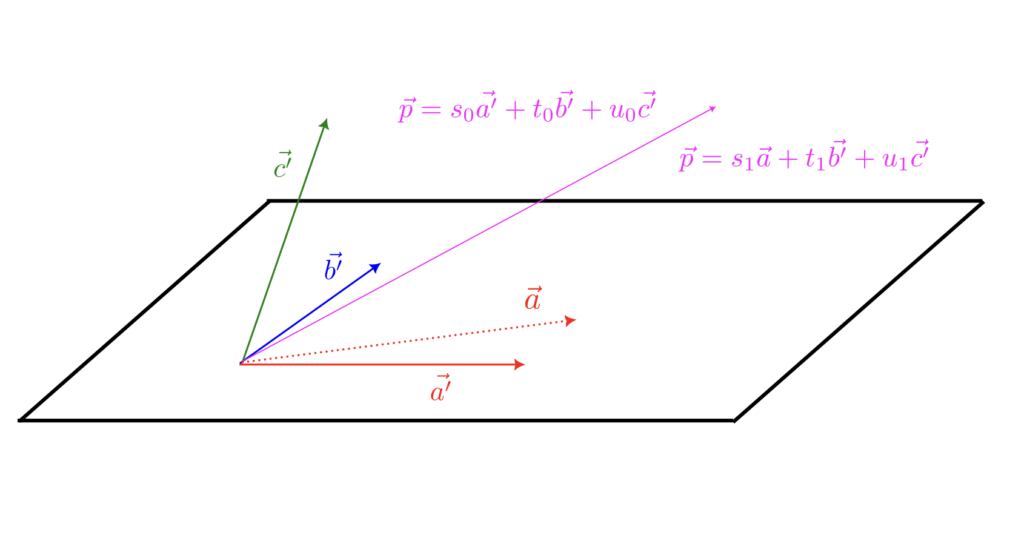
さらに、$\vec{b’}$ → $\vec{b}$, $\vec{c’}$ → $\vec{c}$ としても、$\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}$ の形で表せることを示す。
記号
このページで使う記号を定義する。
$\vec{p}$ が $\vec{a}$ のスカラー倍、すなわちある実数 $s$ に対して $\vec{p} = s\vec{a}$ と表せるとき $\vec{p} \in <\vec{a}>$ と書き、そうでないとき $\vec{p}\notin<\vec{a}>$ と書く。
これは、$\vec{a}\neq\vec{0}$ とすると、$\vec{p}$ が $\vec{a}$ と同一直線上にある場合、$\vec{p} \in <\vec{a}>$ と書ける。
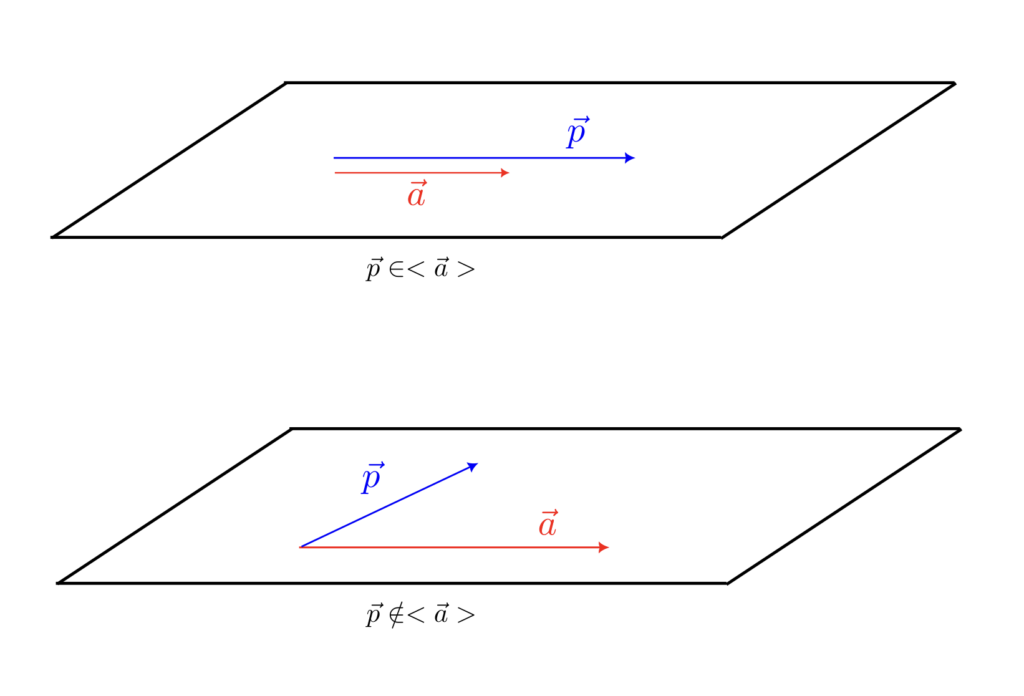
$\vec{p}$ が $\vec{a}$ のスカラー倍と $\vec{b}$ のスカラー倍の和、すなわちある実数 $s,t$ に対して、$\vec{p} = s\vec{a} + t\vec{b}$ と表せるとき、$\vec{p}\in<\vec{a},\vec{b}>$ と書き、そうでないとき $\vec{p}\notin <\vec{a},\vec{b}>$ と書く。
これは、$\vec{a}$ と $\vec{b}$ が1次独立、すなわち零ベクトルでない $\vec{a}$ と $\vec{b}$ が同一直線上にないとすると、$\vec{p}$ が $\vec{a}$ と $\vec{b}$ と同一平面上にある場合、$\vec{p}\in<\vec{a},\vec{b}>$ と書ける。
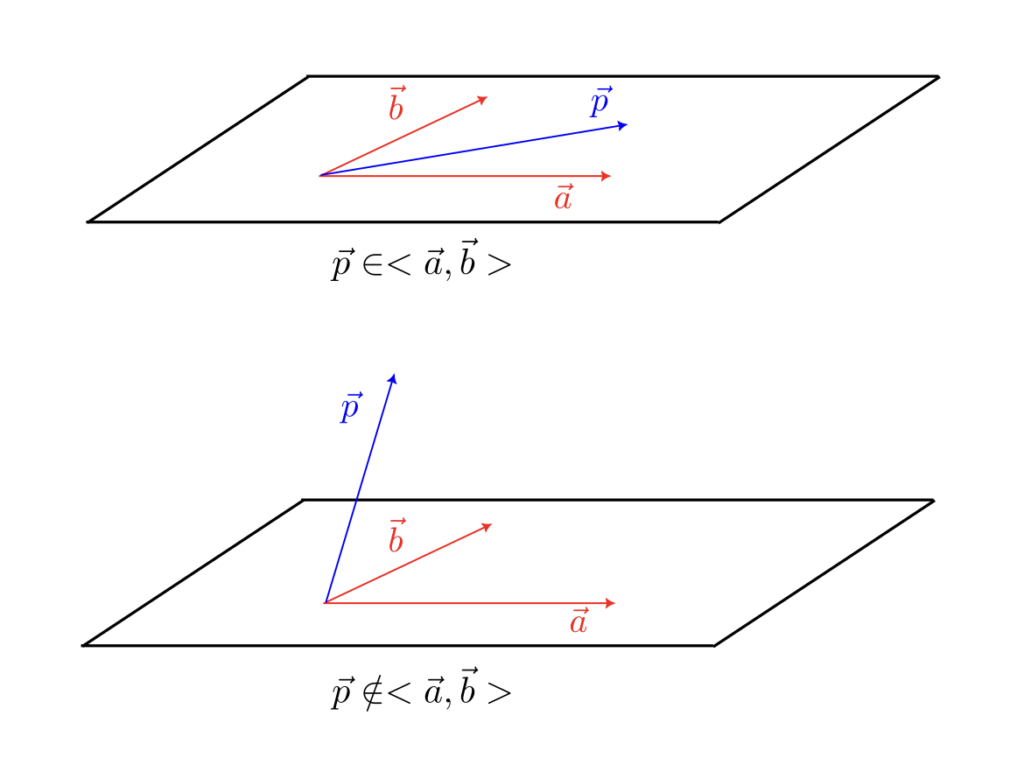
$\vec{p}$ が $\vec{a}$ のスカラー倍と $\vec{b}$ のスカラー倍と $\vec{c}$ のスカラー倍の和、すなわちある実数 $s,t,u$ に対して、$\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}$ と表せるとき、$\vec{p}\in<\vec{a},\vec{b},\vec{c}>$ と書き、そうでないとき $\vec{p}\notin<\vec{a},\vec{b},\vec{c}>$ と書く。
いくつかの補題
目標の定理を証明する前にいくつかの補題を証明する。
補題1
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立であるとする。
また、空間上のベクトル $\vec{d}$ は $\vec{d}\in<\vec{a},\vec{b},\vec{c}>$ かつ $\vec{d}\notin<\vec{b}, \vec{c}>$ とする。
このとき、 $\vec{d}$ と $\vec{b}$ と $\vec{c}$ は1次独立であり、任意の $\vec{p}\in<\vec{a}, \vec{b},\vec{c}>$ に対して、$\vec{p}\in<\vec{d},\vec{b}, \vec{c}>$ である。
証明
$\vec{d}\notin<\vec{b}, \vec{c}>$ より $\vec{d}$ と $\vec{b}$ と $\vec{c}$ は1次独立である。
(空間ベクトル2を参照)
任意に $\vec{p}\in<\vec{a},\vec{b},\vec{c}>$ をとる。
$\vec{p}$ は
$$
\vec{p} = s\vec{a} + t\vec{b} + u\vec{c} \tag{1}\label{1}
$$
と表せる。
また、$\vec{d}\in<\vec{a},\vec{b},\vec{c}>$ より、$\vec{d} = s’\vec{a} + t’\vec{b} + u’\vec{c}$ と表せる。
$\vec{d}\notin<\vec{b}, \vec{c}>$ より、$s’\neq 0$ である。
よって、
$$
\vec{a} = \frac{1}{s’}\vec{d} – \frac{t’}{s’}\vec{b} – \frac{u’}{s’}\vec{c}
$$
となる。
よって、これを $(\ref{1})$ に代入すると、
$$
\begin{align}
\vec{p} &= s\vec{a} + t\vec{b} + u\vec{c} \\
&= s\left(\frac{1}{s’}\vec{d} – \frac{t’}{s’}\vec{b} – \frac{u’}{s’}\vec{c}\right) + t\vec{b} + u\vec{c} \\
&= \frac{s}{s’}\vec{d} + \left(-\frac{st’}{s’} + t\right)\vec{b} + + \left(-\frac{su’}{s’} + u\right)\vec{c}
\end{align}
$$
となるので、$\vec{p}\in<\vec{d},\vec{b}, \vec{c}>$ となる。
補題2
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立、$\vec{d} \neq \vec{0}$ とする。
このとき、$\vec{d} \in<\vec{a}, \vec{b}>$ かつ $\vec{d} \in<\vec{b}, \vec{c}>$ かつ $\vec{d} \in<\vec{c}, \vec{a}>$ となる事はない。
すなわち、$\vec{d} \notin<\vec{a}, \vec{b}>$ または $\vec{d} \notin<\vec{b}, \vec{c}>$ または $\vec{d} \notin<\vec{c}, \vec{a}>$ である。
証明
$\vec{d} \in<\vec{a}, \vec{b}>$ かつ $\vec{d} \in<\vec{b}, \vec{c}>$ かつ $\vec{d} \in<\vec{c}, \vec{a}>$ とする。
$\vec{d} \in<\vec{a}, \vec{b}>$ かつ $\vec{d} \in<\vec{b}, \vec{c}>$ ならば
$$
\vec{d} = s_1\vec{a} + t_1\vec{b}
$$
かつ
$$
\vec{d} = t_2\vec{b} + u_2\vec{c}
$$
と書ける。よって、$s_1\vec{a} + t_1\vec{b} = t_2\vec{b} + u_2\vec{c}$ より
$$
s_1\vec{a} + (t_1 – t_2)\vec{b} – u_2\vec{c} = \vec{0}
$$
であり、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立なので、$s_1 = u_2 = 0$ かつ $t_1 = t_2$ である。
よって、$\vec{d} = t\vec{b}$ と表すことが出来て、$\vec{d}$ は $\vec{b}$ と同一直線上である。
また、$\vec{d} \in<\vec{c}, \vec{a}>$ なら
$$
\vec{d} = s_3\vec{a} + u_3\vec{c}
$$
と表せるので、$t\vec{b} = s_3\vec{a} + u_3\vec{c}$ より
$$
s_3\vec{a} – t\vec{b} + u_3\vec{c} = \vec{0}
$$
となり、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立なので、$s_3 = t = u_3 = 0$ となり、$\vec{d} = \vec{0}$ となってしまい矛盾する。
よって、$\vec{d} \in<\vec{a}, \vec{b}>$ かつ $\vec{d} \in<\vec{b}, \vec{c}>$ かつ $\vec{d} \in<\vec{c}, \vec{a}>$ となることはない。
補題3
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立とする。
また、$\vec{a}$ と $\vec{d}$ も1次独立、すなわち零ベクトルでない $\vec{a}$ と $\vec{d}$ が同一直線上にないとする。
このとき、$\vec{d}\notin<\vec{a},\vec{b}>$ または $\vec{d}\notin<\vec{a},\vec{c}>$ である。
証明
$\vec{d}\in<\vec{a},\vec{b}>$ かつ $\vec{d}\in<\vec{a},\vec{c}>$ であると仮定する。
このとき、$\vec{d} = s_1\vec{a} + t_1\vec{b}$ かつ $\vec{d} = s_2\vec{a} + u_2\vec{c}$ と表せる。
よって、$(s_1 – s_2)\vec{a} + t_1\vec{b} – u_2\vec{c} = \vec{0}$ となる。
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立なので、$t_1 = u_2 = 0$ かつ $s_1 = s_2$ である。
よって、$\vec{d} = s\vec{a}$ となり $\vec{a}$ と $\vec{d}$ が1次独立であることに矛盾するため、$\vec{d}\in<\vec{a},\vec{b}>$ かつ $\vec{d}\in<\vec{a},\vec{c}>$ となる事はない。
よって、このとき、$\vec{d}\notin<\vec{a},\vec{b}>$ または $\vec{d}\notin<\vec{a},\vec{c}>$ である。
定理の証明
まず、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立である $\Rightarrow$ 任意のベクトル $\vec{p}$ に対して、
$$
\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}
$$
と表せること、すなわち $\vec{p}\in<\vec{a},\vec{b},\vec{c}>$ を示す。
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立であるとする。
$\vec{e}_1 = (1,0,0), \vec{e}_2 = (0,1,0), \vec{e}_3 = (0,0,1)$ とすると、$\vec{e}_1$ と $\vec{e}_2$ と $\vec{e}_3$ は1次独立であり、任意のベクトル $\vec{p} = (p_1,p_2,p_3)$ に対して
$$
\vec{p} = p_1\vec{e}_1 + p_2\vec{e}_2 + p_3\vec{e}_3
$$
と表すことが出来るので、$\vec{p}\in<\vec{e}_1,\vec{e}_2,\vec{e}_3>$ となる。
同様に $\vec{a}\in<\vec{e}_1,\vec{e}_2,\vec{e}_3>$ であることも言える。
補題2より、$\vec{a}\notin<\vec{e}_1,\vec{e}_2>$ または $\vec{a}\notin<\vec{e}_2,\vec{e}_3>$ または $\vec{a}\notin<\vec{e}_3,\vec{e}_1>$ である。
例えば、$\vec{a}\notin<\vec{e}_2,\vec{e}_3>$ とすると、補題1より $\vec{a}$ と $\vec{e}_2$ と $\vec{e}_3$ は1次独立であり、$\vec{p}\in<\vec{a},\vec{e}_2,\vec{e}_3>$ となる。
仮定より $\vec{a}$ と $\vec{b}$ は1次独立なので、補題3より $\vec{b}\notin<\vec{a},\vec{e}_2>$ または $\vec{b}\notin<\vec{a},\vec{e}_3>$ である。
よって、補題1より $\vec{p} \in <\vec{a},\vec{b},\vec{e}_3>$ となる。
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立より、$\vec{c}\notin<\vec{a},\vec{b}>$ である。
よって、補題1より $\vec{p}\in<\vec{a},\vec{b},\vec{c}>$ となる。
次に一意性を示す。
$\vec{p}$ を $\vec{p} = s_1\vec{a} + t_1\vec{b} + u_1\vec{c}$ と $\vec{p} = s_2\vec{a} + t_2\vec{b} + u_2\vec{c}$ で表せたとする。
$s_1\vec{a} + t_1\vec{b} + u_1\vec{c} = s_2\vec{a} + t_2\vec{b} + u_2\vec{c}$ より、$(s_1 – s_2)\vec{a} + (t_1 – t_2)\vec{b} + (u_1 – u_2)\vec{c} = \vec{0}$ となる。
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立より、$s_1 – s_2 = 0$ かつ $t_1 – t_2 = 0$ かつ $u_1 – u_2 = 0$ である。
よって、$s_1 = s_2, t_1 = t_2, u_1 = u_2$ となるので、一意性は示された。
最後に、任意の空間ベクトル $\vec{p}$ に対して、
$$
\vec{p} = s\vec{a} + t\vec{b} + u\vec{c}
$$
を満たす $s, t, u$ が唯一つ存在する $\Rightarrow$ $\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立であることを示す。
仮定より、$s\vec{a} + t\vec{b} + u\vec{c} = \vec{0}$ となる $s,t,u$ が唯一つ存在する。
よって、$s = t = u = 0$ は、$s\vec{a} + t\vec{b} + u\vec{c} = \vec{0}$ を満たしそれ以外の値は持たないので、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立である。
補足
(3次元)空間上の任意のベクトル $\vec{p}$ は、1次独立である2つのベクトル $\vec{a}$ と $\vec{b}$ により生成させることはできない。
(すなわち、あるベクトル $\vec{p}$ はどんな実数 $s,t$ を取っても
$$
\vec{p} = s\vec{a} + t\vec{b}
$$
と表すことができない。)
また、どんな4つのベクトルをとってきても、3次元空間では1次独立になることはない。
つまり3次元空間では1次独立であり、任意のベクトルを生成させるために必要なベクトルは3つである。


