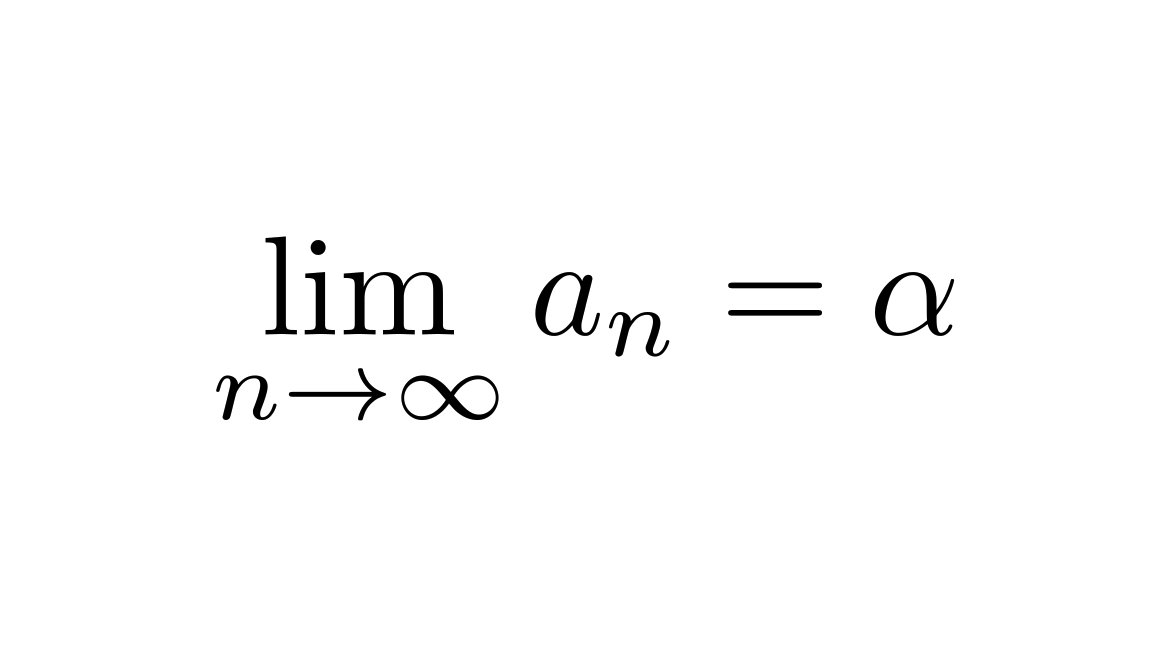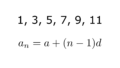事前知識
数列の極限とは
ざっくりいうと数列の極限とは、
数列 $\{a_n\}$ の $n$ をだんだん大きくしていくと、$a_n$ は何の値に近づくか?
というものである。
以下の数列について見てみる。
$$
a_n = \frac{1}{n}
$$
$n$ に適当な値を代入してみると以下のような感じになる。
| $n$ | 1 | 2 | 3 | 10 | 100 | 1000 | 1000000 | 10000000000 | … |
|---|---|---|---|---|---|---|---|---|---|
| $a_n$ | 1 | 0.5 | 0.333… | 0.1 | 0.01 | 0.001 | 0.000001 | 0.0000000001 | … |
感覚的に $n$ を大きくしていくと、 $a_n = \frac{1}{n}$ は 0 に近づいていることが分かる。
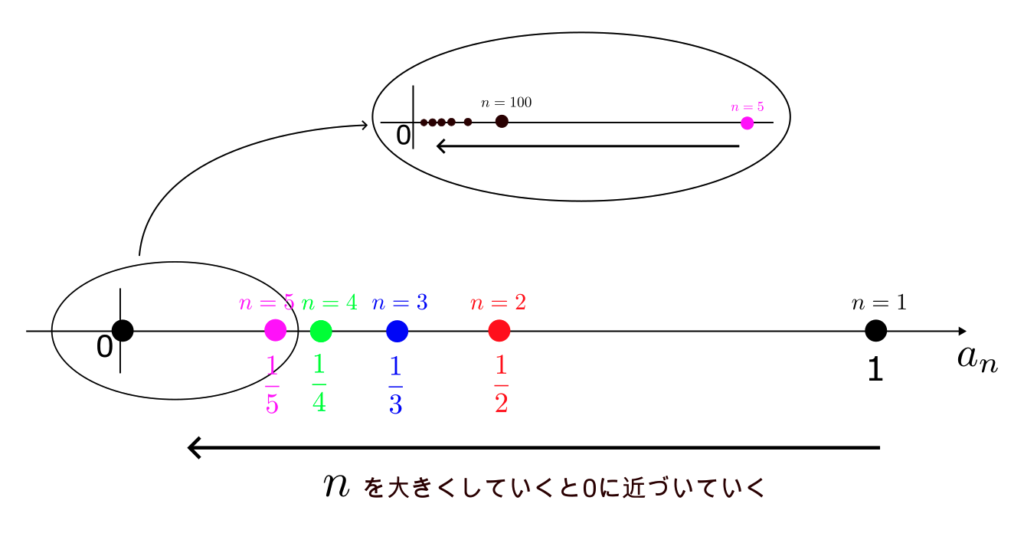
このとき、数列 $\{a_n\}$ は 0 に収束するといい、数式では
$$
\lim_{n\to \infty} \frac{1}{n} = 0
$$
と書く。
定義
「近づく」を具体的に
上記の例ではかなり曖昧な表現を使ったので、実際どのように定義されるのかを見ていく。
上記では「数列 $\{a_n\}$ が 0 に収束する」とは「$n$ を大きくしていくと、$a_n$ は 0 に近づく」と書いた。
では、「$a_n$ は 0 に近づく」をどのように表現するのか。
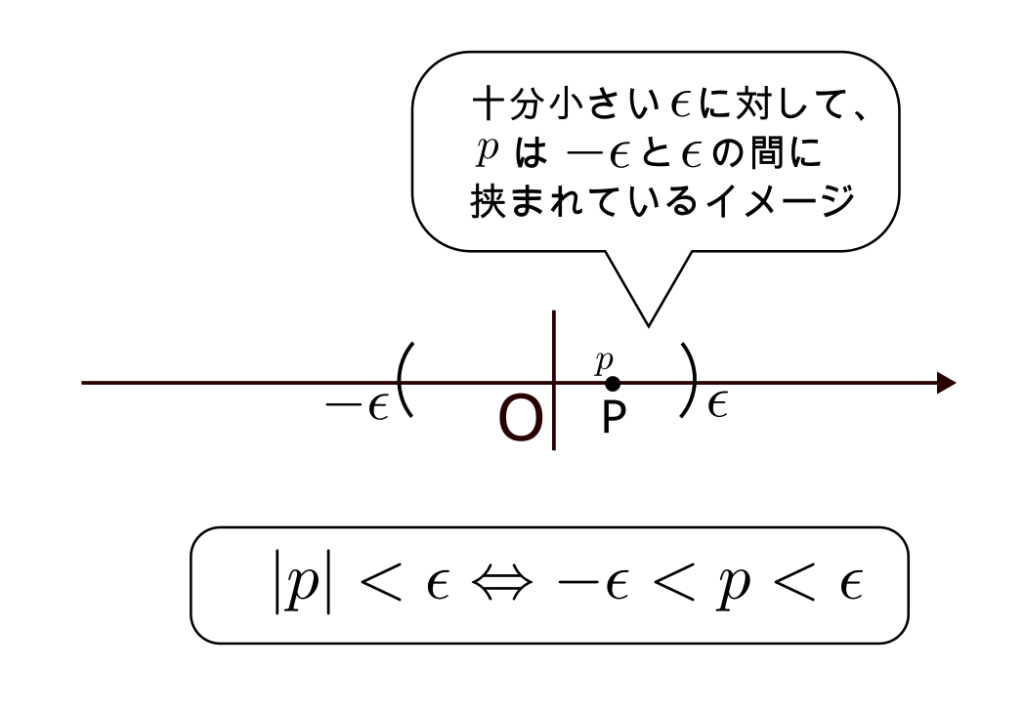
下の図のような点Pが原点Oに近づく場合をPの座標を$p$, Oの座標を 0 として考えてみる。
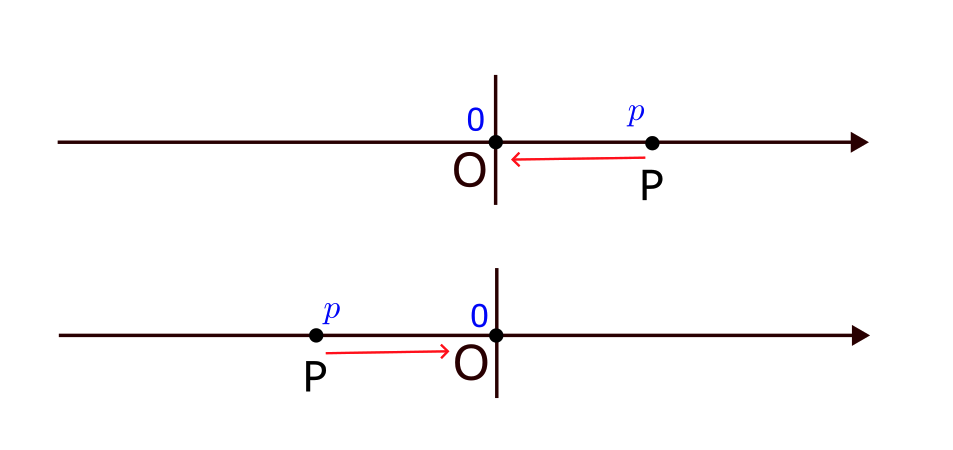
「点Pが原点Oに近づく」すなわち「点Pと原点Oとの距離が限りなく0に近い」ということである。
これを式で
十分小さい正の実数 $\epsilon > 0$ に対して、$|p| < \epsilon$ が成り立つ
と表すことができる。
十分小さいという表現をしたが、「任意の $\epsilon > 0$ に対して、$|p| < \epsilon$」が成り立つとき、「点Pと原点Oとの距離が限りなく0に近い」と言える。
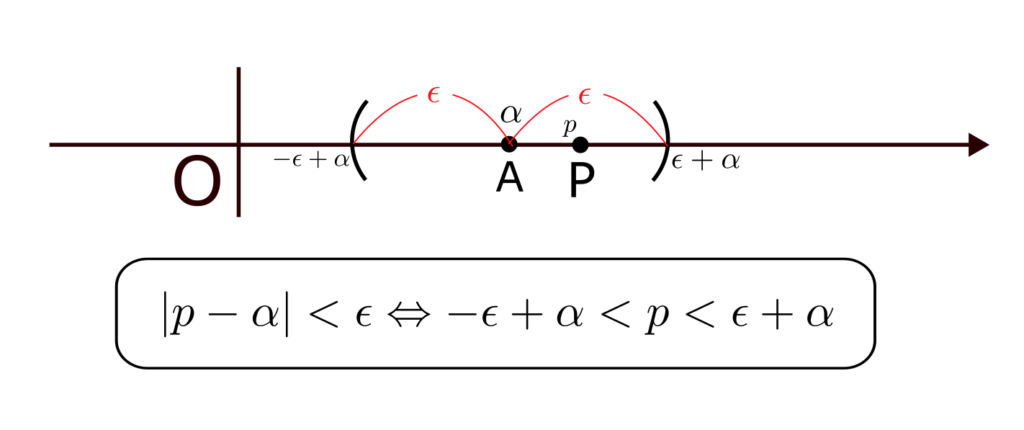
分かりやすくするため、上記では原点に近づく場合を述べたが、点Aの座標を $\alpha$ としたとき、「点Pが点Aに近づく」を言い換えると、
任意の $\epsilon > 0$ に対して、$|p – \alpha| < \epsilon$
となる。
では、「数列 $\{a_n\}$ が $\alpha$ に収束する」はどのように定義されるのか?
「$n$ が十分大きいとき、$a_n$ が $\alpha$ に近づく」を言い換えると、
十分小さい正の実数 $\epsilon$ に対して、$n$ が十分大きいとき、$|a_n – \alpha| < \epsilon$ が成り立つ
となる。
定義
任意の $\epsilon > 0$ に対して、ある自然数 $N$ が存在して、$n \geq N$ を満たすすべての自然数 $n$ に対して、$|a_n – \alpha|<\epsilon$
が成り立つとき、数列 $\{a_n\}$ は $\alpha$ に収束するといい、
$$
\lim_{n\to\infty}a_n = \alpha
$$
と書く。
全称記号を使うと、
$$
\forall \epsilon > 0,\exists N > 0, n\geq N \Rightarrow |a_n – \alpha|<\epsilon
$$
となる。
例
$$
\lim_{n\to\infty} \frac{1}{n} = 0
$$
を定義に沿って示す。
( i ) $\epsilon > 1$ となる $\epsilon$ をとってきた場合
任意の自然数 $n$ に対して、
$$
|a_n| = \left|\frac{1}{n}\right| \leq 1
$$
より、
$$
|a_n| = \left|\frac{1}{n}\right| < \epsilon
$$
が成り立つ。
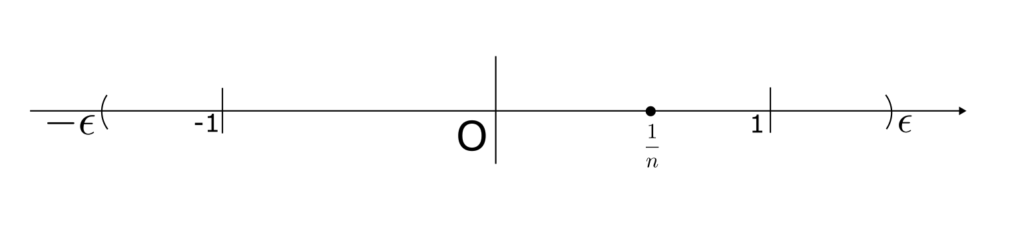
( ii ) $0<\epsilon \leq 1$ となる $\epsilon$ をとってきた場合
$a_n > 0$ であり、
$$
\frac{1}{n} > \frac{1}{n + 1}
$$
すなわち、$a_n > a_{n+1}$ が成り立つ。(つまり、$n$ が大きなると $a_n$ は小さくなっていく。)
よって、
$$
\frac{1}{N} < \epsilon \label{1}\tag{1}
$$
を満たす自然数 $N$ が取れたとき、$n\geq N$ を満たすすべての自然数 $n$ に対して、
$$
|a_n| = \left|\frac{1}{n}\right| < \epsilon
$$
が成り立つ。

$(\ref{1})$ を満たす自然数 $N$ を見つけるには
$$
N > \frac{1}{\epsilon} \label{2}\tag{2}
$$
を満たす自然数 $N$ を見つければいい。$\frac{1}{\epsilon}$ の整数部分を $A_{\epsilon}$ とする。
(例えば、2.31432 の整数部分は 2)
$$
N = A_{\epsilon} + 1
$$
とすると、$(\ref{2})$ が成り立つ。
以上より、
任意の $\epsilon > 0$ に対して、ある自然数 $N$ が存在して、$n \geq N$ を満たすすべての自然数 $n$ に対して、$|\frac{1}{n}|<\epsilon$
が成り立つため、
$$
\lim_{n\to\infty}\frac{1}{n} = 0
$$
となることが示された。