絶対値とは
原点$O$からの距離が $a$ のとき、$a$ の絶対値といい、$|a|$ と書く。
例
|5| = 5
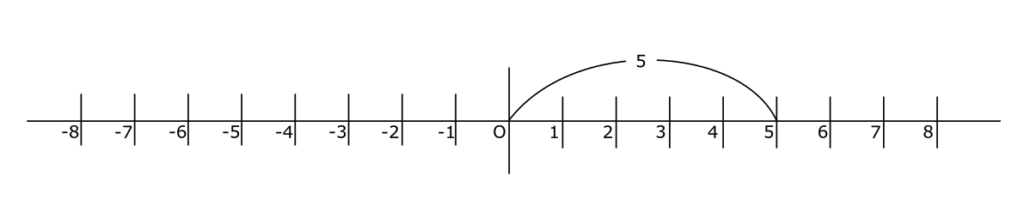
$|-5| = 5$
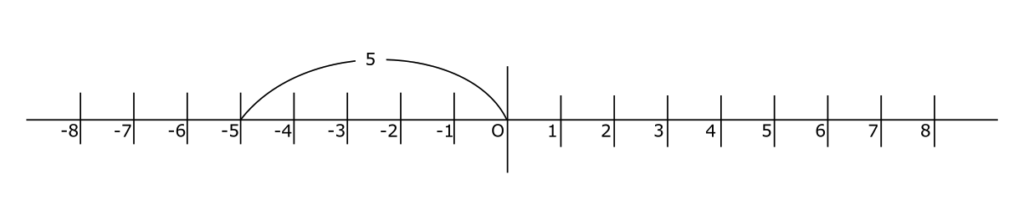
$|1 – \sqrt{2}| = \sqrt{2} – 1$
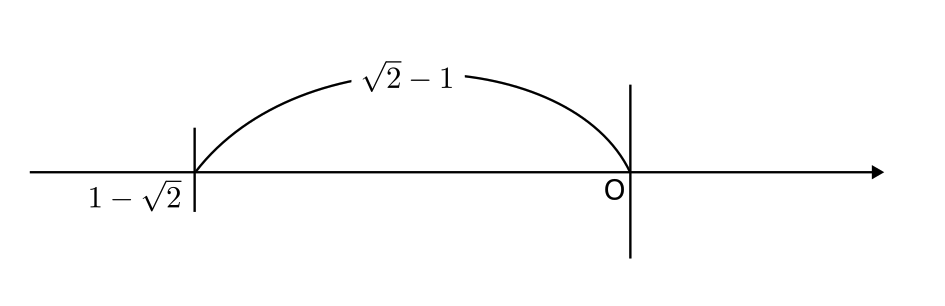
文字で表す
塾でアルバイトをしていたとき、$|a|$を記号を使わずに表すとどうなるか質問してみるとほとんどの生徒は「$|a| = \pm a$」と答えた。
絶対値を使った方程式
$$
|x| = a \Leftrightarrow x = \pm a
$$
とごっちゃになってしまったのかもしれない。
仮に「$|a| = \pm a$」が正しいとすると、$|5| = \pm 5$ となる。
しかし、上の例でやった通り、$|5| = 5$で、絶対値は負の値を取らない。
$|a|$を記号を使わずに表すとどうなるのか?
記号の中が0以上のとき、上記の例でやった通り、記号をそのまま外した値になる。
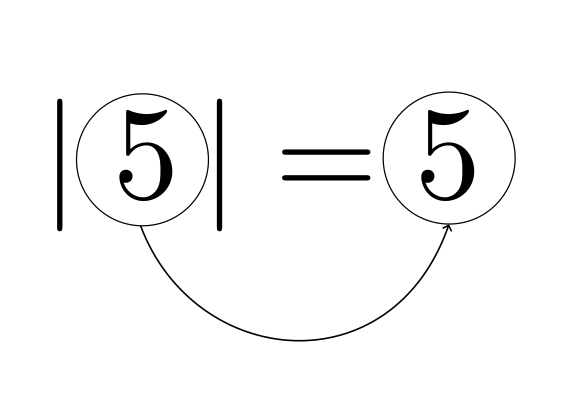
すなわち、
$$
a \geq 0 \text{のとき、}|a| = a
$$
次に記号の中が負のときを考える。
例えば、$|-5|$ は $|-5| = 5$ のように、記号の中の「$-$」を外した値となる。
もう少し具体的に見てみると、5 は $-(-5)$ ともかける。つまり、
$$
|-5| = -(-5) = 5
$$
というように $|-5|$ は記号の中の数に $-1$ をかけた値に等しい。
他の例を見てみると、$|1 – \sqrt{2}|$ も
$$
|1-\sqrt{2}| = -(1-\sqrt{2}) = \sqrt{2} – 1
$$
というように、記号の中の数に $-1$ をかけた値になっている。
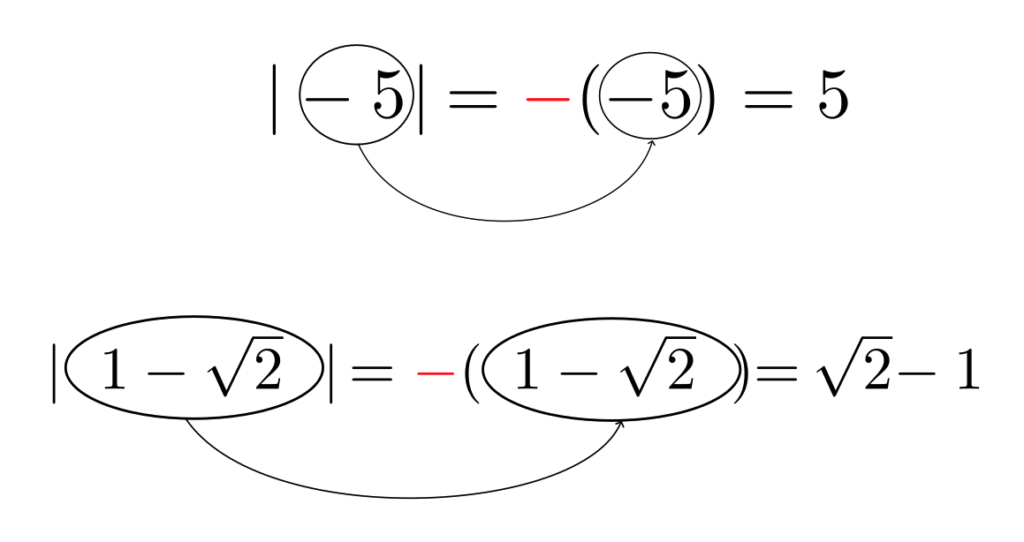
つまり、
$$
a < 0\text{のとき、}|a| = -a
$$
となる。
まとめ
$a \geq 0$ のとき、$|a| = a$
$a < 0$ のとき、$|a| = -a$
すなわち、
$$
|a| =
\left\{
\begin{array}{ll}
a & (a \geq 0)\\
-a & (a < 0)
\end{array}
\right.
$$
と書くことができる。


