事前知識
例1
以下の方程式を解く。
$$
|x| = 3
$$
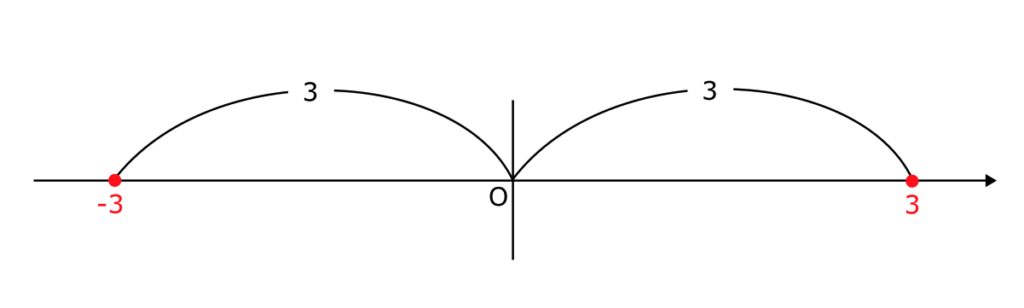
原点から距離が3となる位置は $3$ と $-3$ である。
よって、$x = 3$ または $x = -3$ となる。
少し面倒だが今回の記事では大事な考え方のため、場合分けを使って解いてみる。
$|x|$ を記号を使わずに表すと、
$$
x \geq 0 \text{のとき、}|x| = x
$$
$$
x < 0\text{のとき、}|x| = -x
$$
となる。
$x \geq 0$ のとき、$|x| = 3$ は $x = 3$ となる。
$x < 0$ のとき、$|x| = 3$ は $-x = 3$ となるため、$x = -3$ である。
よって、$|x| = 3$ を解くと、$x = 3$ または $x = -3$ となる。
例2
$$
|x – 3| = 2 \label{1}\tag{1}
$$
この方程式について考える。
$x – 3 \geq 0$ のとき、$|x – 3| = x – 3$ となる。すなわち、$x \geq 3$ のとき、$|x – 3| = x – 3$ となる。
$x – 3 < 0$ のとき、$|x – 3| = -(x – 3)$ となる。すなわち、$x < 3$ のとき、$|x – 3| = -x + 3$ となる。
このことを踏まえて、方程式 $(\ref{1})$ を解いていく。
$x\geq 3$ のとき、$(\ref{1})$ は
$$
\begin{align}
|x-3| &= 2 \\
x-3 &= 2 \\
x &= 5
\end{align}
$$
$x < 3$ のとき、$(\ref{1})$ は
$$
\begin{align}
|x – 3| &= 2 \\
-x + 3 &= 2 \\
x &= 1
\end{align}
$$
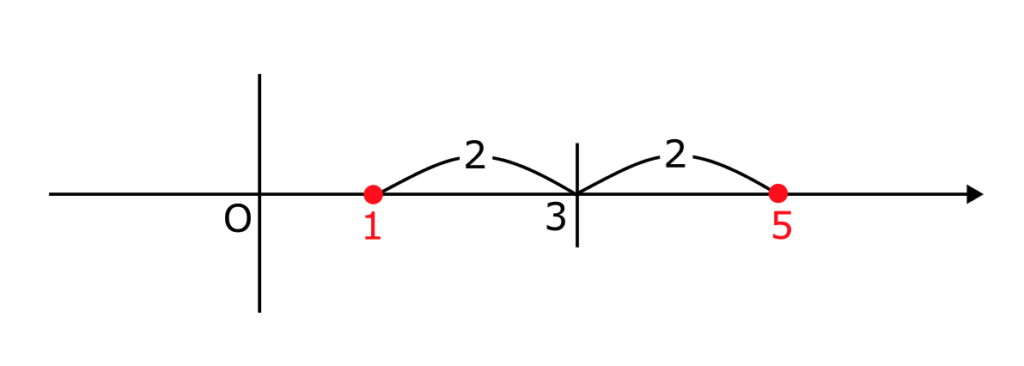
よって、方程式 $(\ref{1})$ の解は $x = 1$ または $x = 5$ である。
これは点3から距離が2である値が解であることを示している。
例3
$$
|x| + |2x – 4| = 5 \label{2} \tag{2}
$$
場合分けすべき境目は絶対値記号の中が0のときである。つまり、$x = 0$ と $2x – 4 = 0$ すなわち $x = 2$ である。
絶対値記号を外した $(\ref{2})$ の左辺の式は$x \geq 2$ の場合と $0 \leq x < 2$ の場合と $x < 0$ の場合とでそれぞれ異なる。
$x \geq 2$ の場合。
$|x| = x$, $|2x – 4| = 2x – 4$ より
$$
\begin{align}
|x| + |2x – 4| &= 5 \\
x + (2x – 4) &= 5 \\
3x &= 9 \\
x &= 3
\end{align}
$$
$0\leq x < 2$ の場合。
$|x| = x$, $|2x – 4| = – (2x – 4) = -2x + 4$ より
$$
\begin{align}
|x| + |2x – 4| &= 5 \\
x – 2x + 4 &= 5 \\
x &= -1
\end{align}
$$
だが、今は $0\leq x < 2$ の場合について考えていることに注意する。$x = -1$ は $0\leq x < 2$ の中にないため、解ではない。
$x \geq 2$ の場合は、解が $x = 3$ でこれは $x\geq 2$ を満たしているのでOK。
$x < 0$ の場合。
$|x| = -x$, $|2x – 4| = – (2x – 4) = -2x + 4$ より
$$
\begin{align}
|x| + |2x – 4| &= 5 \\
-x – 2x + 4 &= 5 \\
-3x &= 1 \\
x &= -\frac{1}{3}
\end{align}
$$
$x = -\frac{1}{3}$ は $x < 0$ を満たしているため解である。
よって、方程式 $(\ref{2})$ の解は
$$
x = -\frac{1}{3}\text{ または } x = 3
$$
となる。


