三角比

sin, cos, tan

sin(正弦)

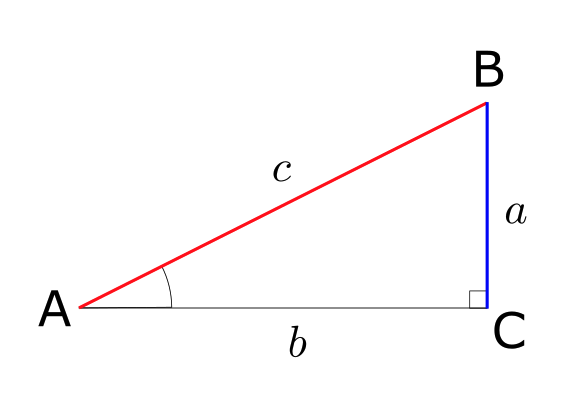
上記の図の赤色の辺と青色の辺の比を \(\angle A\) の正弦といい、以下のように定義する。
$$
\sin A = \frac{\color{blue}{\text{青色の辺}}}{\color{red}{\text{赤色の辺}}} = \frac{a}{c}
$$

cos(余弦)

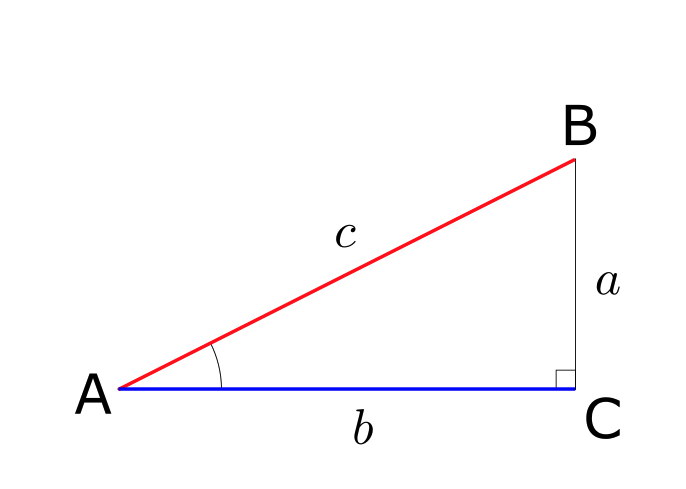
上記の図の赤色の辺と青色の辺の比を \(\angle A\) の余弦といい、以下のように定義する。
$$
\cos A = \frac{\color{blue}{\text{青色の辺}}}{\color{red}{\text{赤色の辺}}} = \frac{a}{b}
$$

tan(正接)

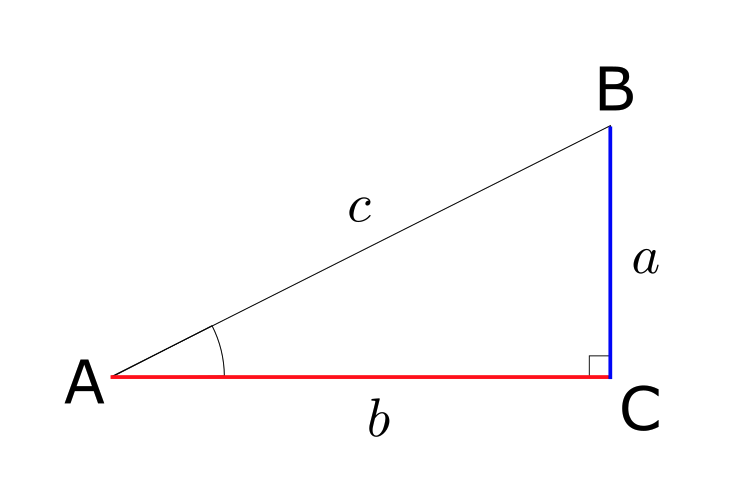
上記の図の赤色の辺と青色の辺の比を \(\angle A\) の正接といい、以下のように定義する。

$$
\tan A = \frac{\color{blue}{\text{青色の辺}}}{\color{red}{\text{赤色の辺}}} = \frac{a}{b}
$$

例

例1

以下のような 3:4:5 の直角三角形を考える。

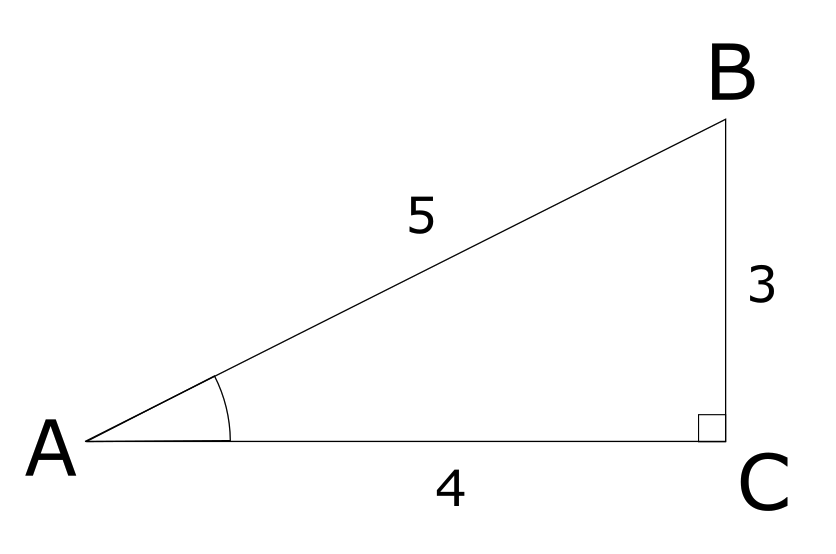
このとき、
$$
\sin A = \frac{3}{5}\ \ \ \cos A = \frac{4}{5}\ \ \ \tan A = \frac{3}{4}
$$

例2(30°)

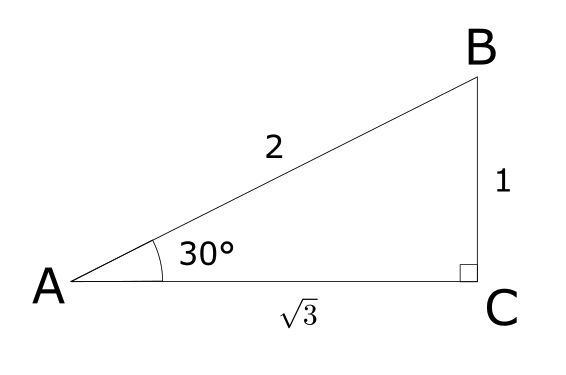
上記のような、斜辺(AB)が2、\(\angle A = 30°\)の直角三角形を考える。このとき、
$$
\sin 30°= \frac{1}{2}\ \ \ \cos 30°= \frac{\sqrt{3}}{2}\ \ \ \tan 30°= \frac{1}{\sqrt{3}}
$$
となる。

例3(45°)

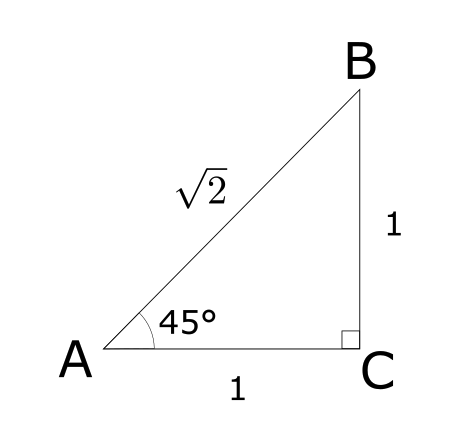
上記のような、斜辺(AB)が\(\sqrt{2}\)、\(\angle A = 45°\)の直角三角形を考える。このとき、
$$
\sin 45°= \frac{1}{\sqrt{2}}\ \ \ \cos 45°= \frac{1}{\sqrt{2}}\ \ \ \tan 45°= 1
$$
となる。

例4(60°)

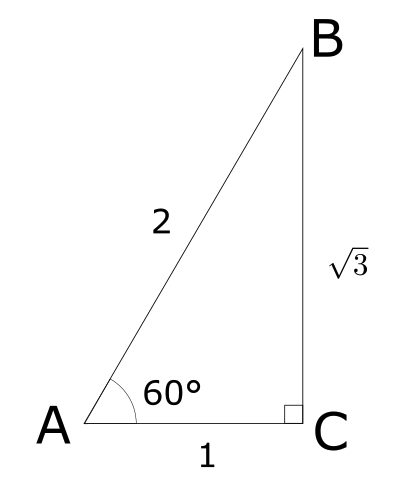
上記のような、斜辺(AB)が2、\(\angle A = 60°\)の直角三角形を考える。このとき、
$$
\sin 60°= \frac{\sqrt{3}}{2}\ \ \ \cos 60°= \frac{1}{2}\ \ \ \tan 60°= \sqrt{3}
$$
となる。

まとめ

	30°	45°	60°
sin(正弦)	\(\frac{1}{2}\)	\(\frac{1}{\sqrt{2}}\)	\(\frac{\sqrt{3}}{2}\)
cos(余弦)	\(\frac{\sqrt{3}}{2}\)	\(\frac{1}{\sqrt{2}}\)	\(\frac{1}{2}\)
tan(正接)	\(\frac{1}{\sqrt{3}}\)	1	\(\sqrt{3}\)

補足

相似条件より、2つの直角三角形の直角以外の内角の1つがそれぞれ等しい場合、辺の比もそれぞれ等しい。
そのため、どんな大きさの直角三角形を考えたとしても三角比の値は変わらない。

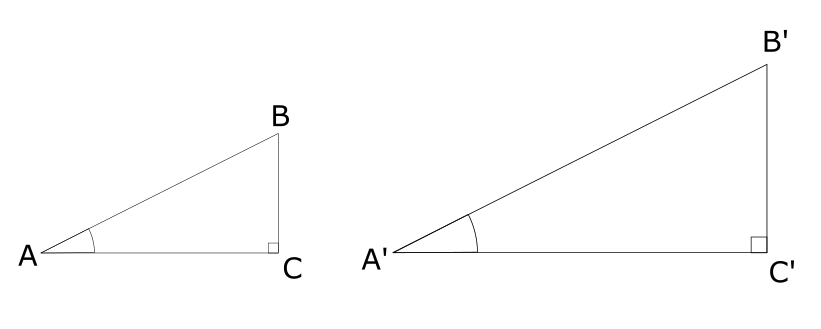
つまり、上記の図で、
$$
\angle \text{A} = \angle \text{A’}
$$
ならば、\(\triangle \text{ABC}\) と \(\triangle \text{A’B’C’}\) は相似であり、
$$
\sin \text{A} = \sin \text{A’},\ \ \ \cos \text{A} = \cos \text{A’},\ \ \ \tan \text{A} = \tan \text{A’}
$$
である。