事前知識
公式
$$
\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta
$$
$$
\sin(\alpha – \beta) = \sin\alpha\cos\beta – \cos\alpha\sin\beta
$$
$$
\cos(\alpha + \beta) = \cos\alpha\cos\beta – \sin\alpha\sin\beta
$$
$$
\cos(\alpha – \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta
$$
$$
\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 – \tan\alpha\tan\beta}
$$
$$
\tan(\alpha – \beta) = \frac{\tan\alpha – \tan\beta}{1 + \tan\alpha\tan\beta}
$$
証明
まず
$$
\cos(\alpha – \beta) = \cos\alpha\cos\beta + \sin\alpha\sin\beta
$$
を示す。
図のように角度 $\alpha$ と $\beta$ をとる。
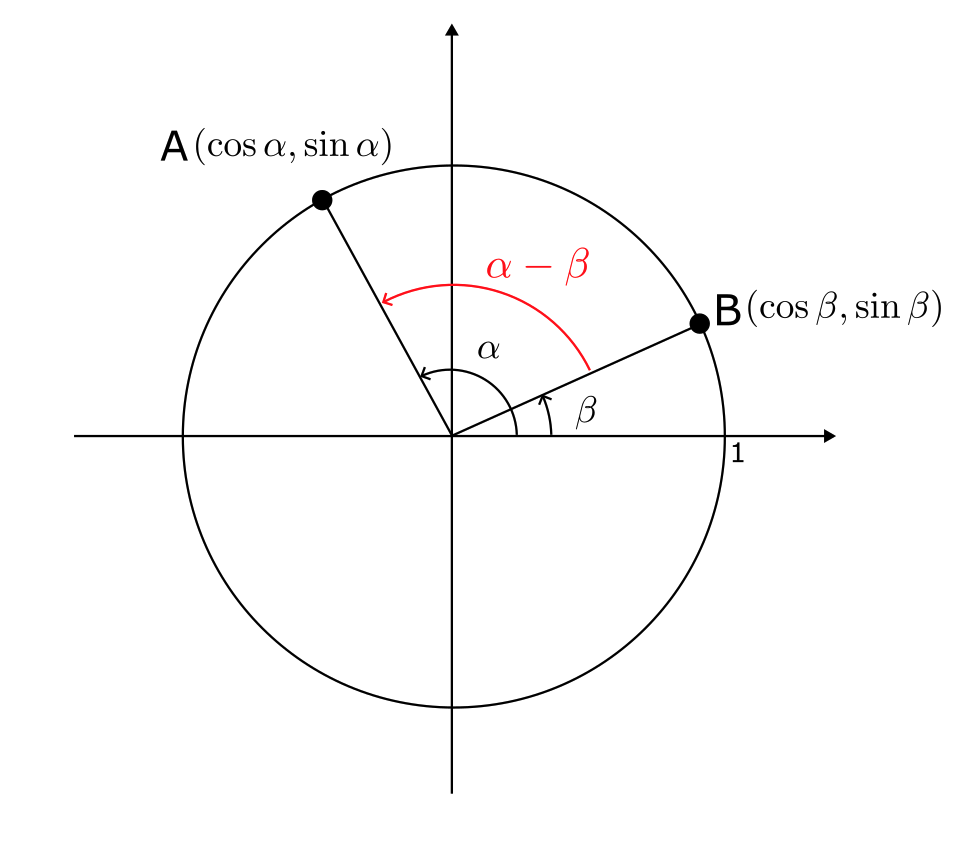
二点間ABの距離の二乗は
$$
\begin{align}
AB^2 &= (\cos\alpha – \cos\beta)^2 + (\sin\alpha – \sin\beta)^2 \\
&= (\cos^2\alpha – 2\cos\alpha\cos\beta + \cos^2\beta) + (\sin^2\alpha – 2\sin\alpha\sin\beta + \sin^2\beta) \\
&= (\sin^2\alpha + \cos^2\alpha) + (\sin^2\beta + \cos^2\beta) – 2\cos\alpha\cos\beta – 2\sin\alpha\sin\beta \\
&= 2 – 2\cos\alpha\cos\beta – 2\sin\alpha\sin\beta
\end{align}
$$
下記の図のように、原点を中心に点Aと点Bから $-\beta$ 回転させる。回転させた点をそれぞれA’とB’とする。
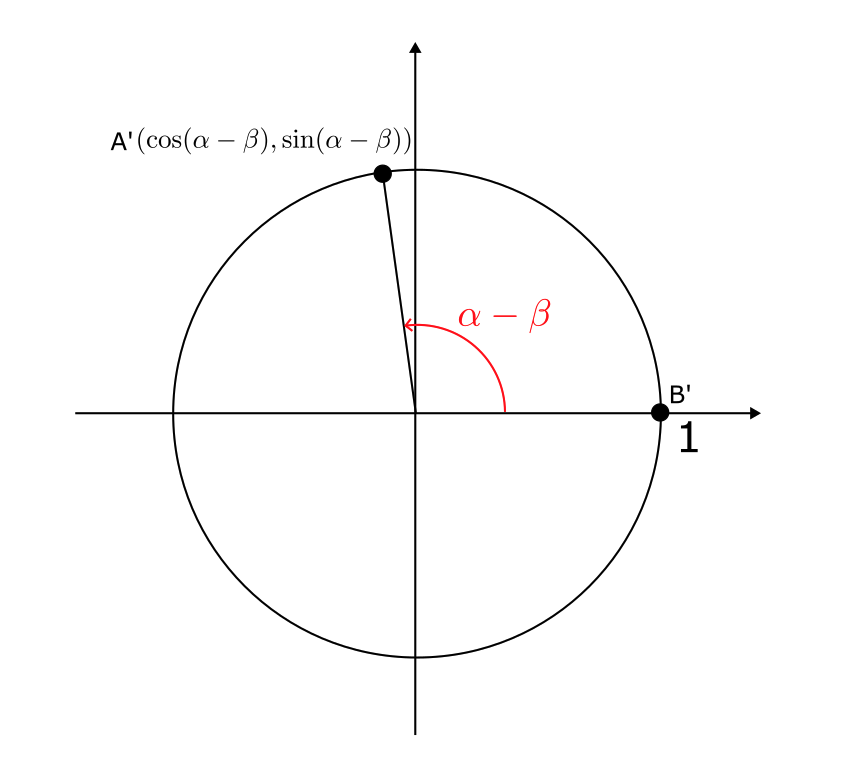
このとき、点A’は $(\cos(\alpha – \beta), \sin(\alpha – \beta))$, 点B’は $(1,0)$ となる。
よって、A’B’の距離の二乗は
$$
\begin{align}
A’B’^2 &= (\cos(\alpha – \beta) – 1)^2 + \sin^2(\alpha – \beta) \\
&=\cos^2(\alpha – \beta) – 2\cos(\alpha – \beta) + 1 + \sin^2(\alpha – \beta) \\
&= (\cos^2(\alpha – \beta) + \sin^2(\alpha – \beta)) + 1 – 2\cos(\alpha – \beta) \\
&= 2 – 2\cos(\alpha – \beta)
\end{align}
$$
となる。
$AB^2 = A’B’^2$ より
$$
\begin{align}
2 – 2\cos\alpha\cos\beta – 2\sin\alpha\sin\beta &= 2 – 2\cos(\alpha – \beta) \\
\cos(\alpha – \beta) &= \cos\alpha\cos\beta + \sin\alpha\sin\beta
\end{align}
$$
となる。
次に、
$$
\cos(\alpha + \beta) = \cos\alpha\cos\beta – \sin\alpha\sin\beta
$$
を示す。
$$
\begin{align}
\cos(\alpha + \beta) &= \cos(\alpha – (-\beta)) \\
&= \cos\alpha\cos(-\beta) + \sin\alpha\sin(-\beta) \\
&= \cos\alpha\cos\beta – \sin\alpha\sin\beta
\end{align}
$$
次に、
$$
\sin(\alpha + \beta) = \sin\alpha\cos\beta + \cos\alpha\sin\beta
$$
を示す。
$$
\sin\theta = \cos\left(\frac{\pi}{2} – \theta\right)
$$
を利用する。
$$
\begin{align}
\sin(\alpha + \beta) &= \cos\left(\frac{\pi}{2} – (\alpha + \beta)\right) \\
&= \cos\left(\left(\frac{\pi}{2} – \alpha\right) – \beta\right)\\
&= \cos\left(\frac{\pi}{2} – \alpha\right)\cos\beta + \sin\left(\frac{\pi}{2} – \alpha\right)\sin\beta \\
&=\sin\alpha\cos\beta + \cos\alpha\sin\beta
\end{align}
$$
次に、
$$
\sin(\alpha – \beta) = \sin\alpha\cos\beta – \cos\alpha\sin\beta
$$
を示す。
$$
\begin{align}
\sin(\alpha – \beta) &= \sin(\alpha + (-\beta)) \\
&= \sin\alpha\cos(-\beta) + \cos\alpha\sin(-\beta) \\
&= \sin\alpha\cos\beta – \cos\alpha\sin\beta
\end{align}
$$
最後に
$$
\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 – \tan\alpha\tan\beta}
$$
と
$$
\tan(\alpha – \beta) = \frac{\tan\alpha – \tan\beta}{1 + \tan\alpha\tan\beta}
$$
を示す。
$$
\begin{align}
\tan(\alpha + \beta) &= \frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)} \\
&= \frac{\sin\alpha\cos\beta + \cos\alpha\sin\beta}{\cos\alpha\cos\beta – \sin\alpha\sin\beta}
\end{align}
$$
ここで、分母と分子から $\cos\alpha\cos\beta$ を割ると、
$$
\begin{align}
\frac{\sin\alpha\cos\beta + \cos\alpha\sin\beta}{\cos\alpha\cos\beta – \sin\alpha\sin\beta} &= \frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta} + \frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{1-\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}} \\
&= \frac{\tan\alpha + \tan\beta}{1 – \tan\alpha\tan\beta}
\end{align}
$$
よって、
$$
\tan(\alpha + \beta) = \frac{\tan\alpha + \tan\beta}{1 – \tan\alpha\tan\beta}
$$
となる。
$$
\tan(\alpha – \beta) = \frac{\tan\alpha – \tan\beta}{1 + \tan\alpha\tan\beta}
$$
も同様に示すことができる。
$$
\begin{align}
\tan(\alpha – \beta) &= \frac{\sin(\alpha-\beta)}{\cos(\alpha-\beta)} \\
&= \frac{\sin\alpha\cos\beta – \cos\alpha\sin\beta}{\cos\alpha\cos\beta + \sin\alpha\sin\beta} \\
&= \frac{\frac{\sin\alpha\cos\beta}{\cos\alpha\cos\beta} – \frac{\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{1+\frac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}} \\
&= \frac{\tan\alpha – \tan\beta}{1 + \tan\alpha\tan\beta}
\end{align}
$$
例
$$
\begin{align}
\sin{\frac{\pi}{12}} &= \sin\left(\frac{\pi}{3} – \frac{\pi}{4}\right) \\
&= \sin\frac{\pi}{3}\cos\frac{\pi}{4} – \cos\frac{\pi}{3}\sin\frac{\pi}{4} \\
&= \frac{\sqrt{3}}{2}\cdot\frac{1}{\sqrt{2}} – \frac{1}{2}\cdot\frac{1}{\sqrt{2}} \\
&= \frac{\sqrt{3} – 1}{2\sqrt{2}} \\
&=\frac{\sqrt{6} – \sqrt{2}}{4}
\end{align}
$$
$$
\begin{align}
\cos{\frac{\pi}{12}} &= \cos\left(\frac{\pi}{3} – \frac{\pi}{4}\right) \\
&= \cos\frac{\pi}{3}\cos\frac{\pi}{4} + \sin\frac{\pi}{3}\sin\frac{\pi}{4} \\
&= \frac{1}{2}\cdot\frac{1}{\sqrt{2}} + \frac{\sqrt{3}}{2}\cdot\frac{1}{\sqrt{2}} \\
&= \frac{1 + \sqrt{3}}{2\sqrt{2}} \\
&=\frac{\sqrt{2} + \sqrt{6}}{4}
\end{align}
$$
$$
\begin{align}
\tan{\frac{\pi}{12}} &= \tan\left(\frac{\pi}{3} – \frac{\pi}{4}\right) \\
&= \frac{\tan\frac{\pi}{3} – \tan\frac{\pi}{4}}{1 + \tan\frac{\pi}{3}\tan\frac{\pi}{4}} \\
&= \frac{\sqrt{3} – 1}{1 + \sqrt{3}} \\
&= 2 – \sqrt{3}
\end{align}
$$
最後の等式は有理化を行った。


