※ この記事はnoteをやっていた頃に投稿した記事です。こちらのブログに移しました。
(note投稿時期:2023年3月14日)
事前知識
組み合わせCについて
$$
_nC_k = \frac{_nP_r}{k!} = \frac{n\times (n-1)\times \cdots \times (n – (k – 1))}{k\times (k-1)\times \cdots \times 1}
$$
だった。
この
$$
\frac{n\times (n-1)\times \cdots \times (n – (k – 1))}{k\times (k-1)\times \cdots \times 1}
$$
を少し変形すると、
$$
\begin{split}
& \frac{n\times (n-1)\times \cdots \times (n – (k – 1))\times (n-k)\times \cdots \times 1}{(k\times (k-1)\times \cdots \times 1)\times ((n-k)\times \cdots \times 1)} \
=&\ \frac{n!}{k!(n-k)!}
\end{split}
$$
となる。つまり、
$$
_nC_k = \frac{n!}{k!(n-k)!} = {}_nC_{n-k}
$$
また、$k=0$のとき、
$$
_nC_0 = 1
$$
である。
※ $0! = 1$についての話はしていないので、今回はあまり触れないが、$_nC_0 = 1$はこのようにした方が都合がいいからである。
$$
_nC_n = \frac{n\times (n-1)\times \cdots \times 1}{n\times (n-1)\times \cdots \times 1} = 1
$$
なので、
$$
_nC_k = {}_nC_{n-k}
$$
を$k = 0$まで拡張すると、
$$
_nC_0 = {}_nC_{n} = 1
$$
となる。
パスカルの三角形
パスカルの三角形とは以下のようなものである。
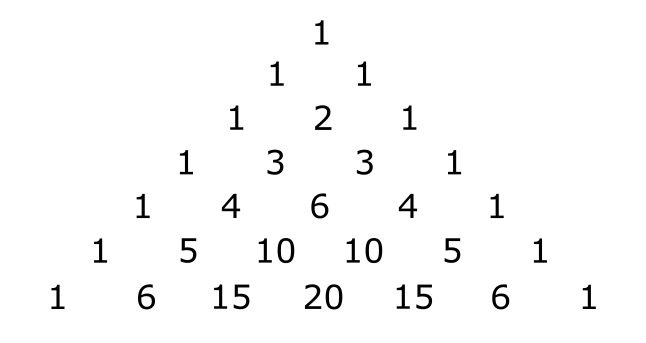
図2のように、各段の両端は1であり、それ以外は隣り合い通しの数の和が下の段の数になる。
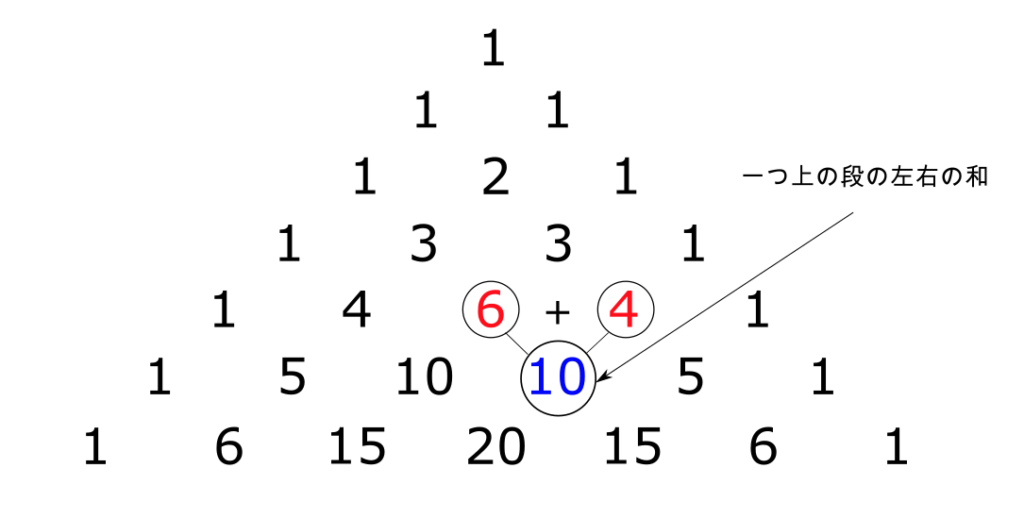
そして、これらの数字は「C」を用いて以下のように書き換えることができる。

例えば、図2と図3の上から6, 左から4つ目の数(図2の青色の所)に注目すると、
$$
_5C_3 = \frac{5\times 4\times 3}{3\times 2\times 1} = 10
$$
で図2と図3が一致していることがわかる。
なぜ一致しているのか?
まず、各段の両端に着目してみると、
$$
_nC_0 = {}_nC_n = 1
$$
となり、図2と図3が一致している事がわかる。
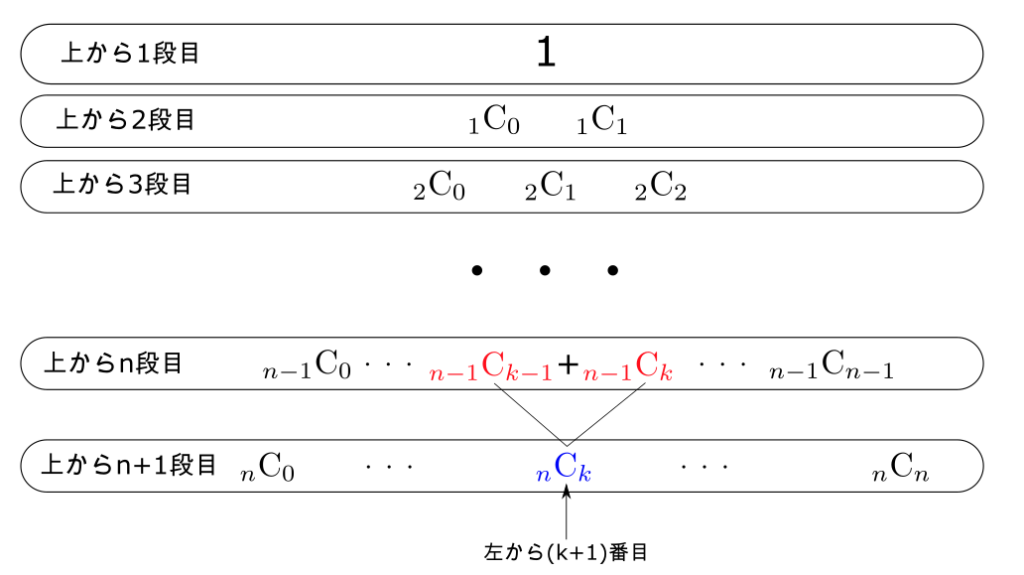
なので、あとは$k=1,\cdots, n-1$に対して、
$$
_nC_k={}_{n-1}C_{k-1} + {}_{n-1}C_k
$$
となっている事を確かめることができればいい。
$$
_nC_k = \frac{n!}{k!(n-k)!}
$$
だったので、
$$
_{n-1}C_{k-1} = \frac{(n-1)!}{(n-k)!(k-1)!},\ {}_{n-1}C_k = \frac{(n-1)!}{(n-k-1)!k!}
$$
となる。よって、
$$
\begin{split}
_{n-1}C_{k-1} + {}_{n-1}C_k &= \frac{(n-1)!}{(n-k)!(k-1)!} + \frac{(n-1)!}{(n-k-1)!k!} \\
&= \frac{(n-1)!(n-k-1)!k!+(n-1)!(n-k)!(k-1)!}{(n-k)!(k-1)!(n-k-1)!k!} \\
&= \frac{(n-1)!(n-k-1)!k(k-1)!+(n-1)!(n-k)(n-k-1)!(k-1)!}{(n-k)!(k-1)!(n-k-1)!k!} \\
&= \frac{(n-1)!(n-k-1)!(k-1)!(k+(n-k))}{(n-k)!(k-1)!(n-k-1)!k!} \\
&= \frac{n!}{(n-k)!k!} \\
&= {}_nC_k
\end{split}
$$
Cが整数になる理由
数学的帰納法を用いて示す。
仮に$n\geqq 2$に対して、
$$
{}_{n-1}C_k\ \ \ (k = 0, 1, \dots,n-1)
$$
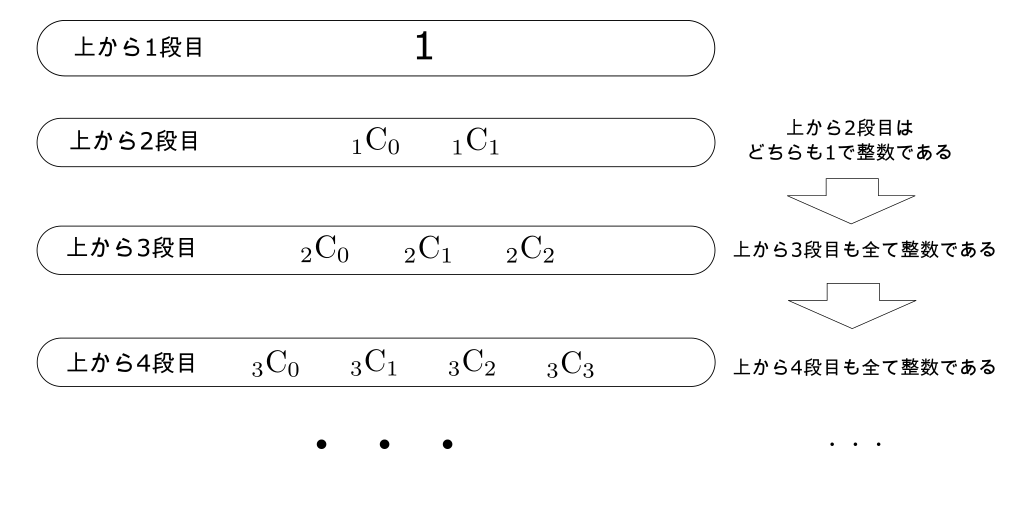
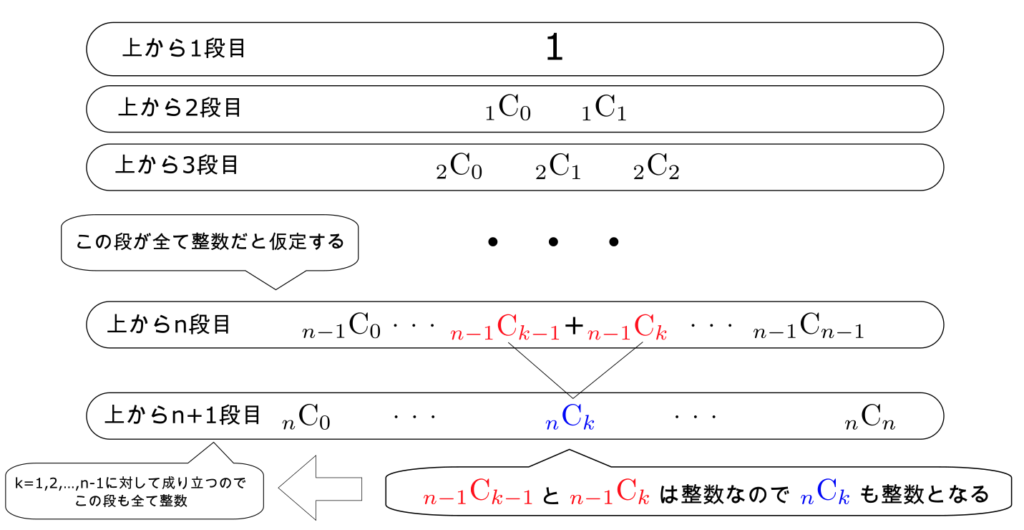
が整数とする。(つまり、パスカルの三角形の上から$n$段目が全て整数だとする。)
$$
_nC_0 = {}_nC_n = 1
$$
で、$k = 1,2,\cdots, n-1$に対し、
$$
_nC_k={}_{n-1}C_{k-1} + {}_{n-1}C_k
$$
だった。仮定から、${}_{n-1}C_{k-1}$と${}_{n-1}C_k$は整数なので、
$$
_nC_k\ \ \ (k = 0,1,\cdots,n)
$$
も整数となる。(つまり、パスカルの三角形の$n$段目が全て整数なら$n+1$段目も全て整数となる。)
また、
$$
_1C_0 = {}_1C_1 = 1
$$
以上のことから、
$_1C_0 = {}_1C_1 = 1$(整数)
⇨ $_2C_k\ \ \ (k = 0,1,2)$も整数
⇨ $_3C_k\ \ \ (k = 0,1,2,3)$も整数
⇨ $_4C_k\ \ \ (k = 0,1,2,3,4)$も整数
⇨ ・・・
という感じになるので、全ての自然数$n$に対して、
$$
_nC_k\ \ \ (k = 0,1,\cdots, n)
$$
は整数になる(もっと言うと、自然数になる)。