前提知識
度数法
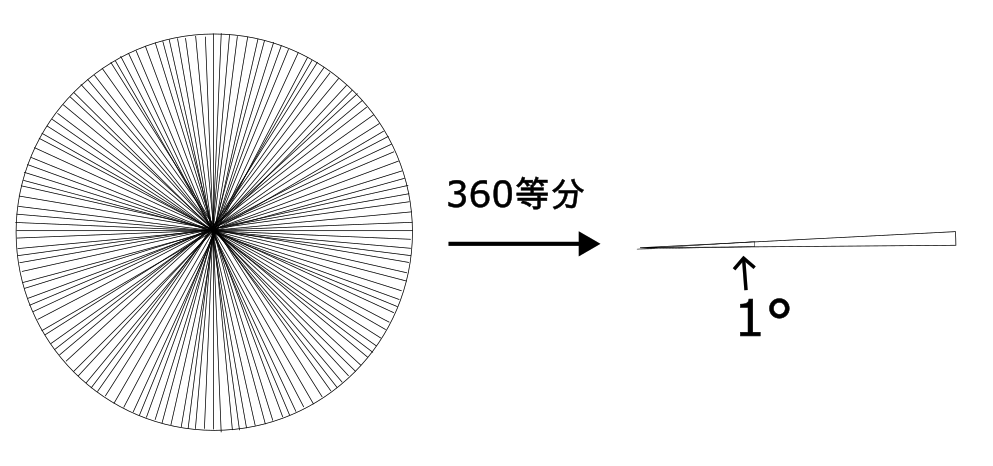
円周を360等分した時の角度を1度(1°)とする。
弧度法
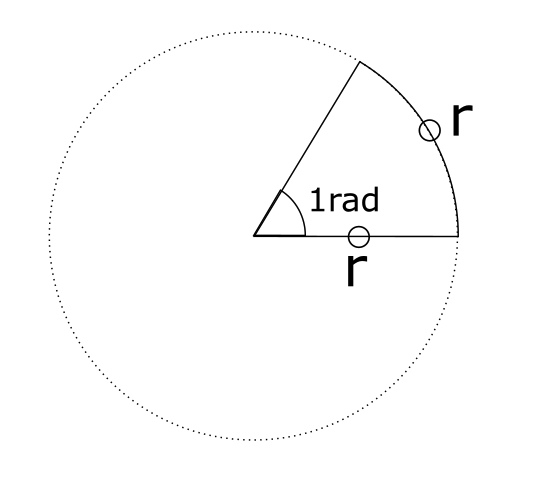
半径と弧の長さが等しい扇形を考える。
このときに出来る中心角を1ラジアン(1 rad)とする。
円周率
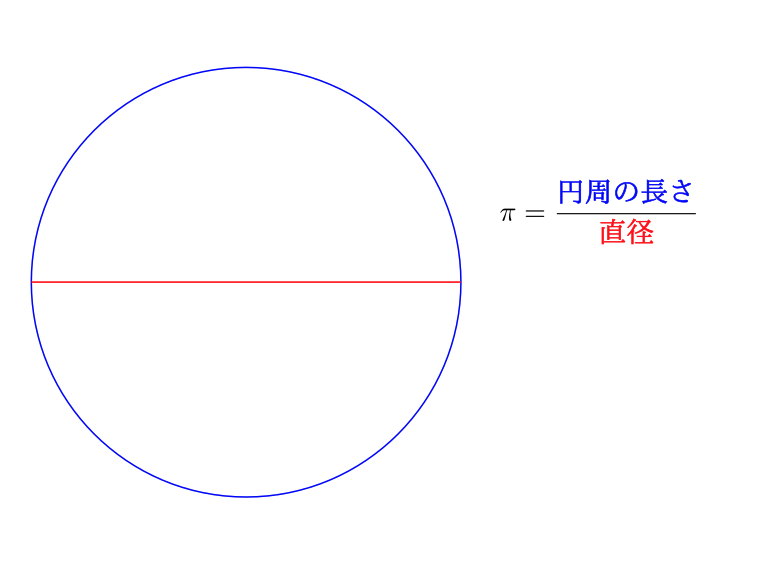
直径と円周の長さの比率$\frac{\text{円周の長さ}}{\text{直径の長さ}}$を円周率と呼び $\pi$ と書く。
半径 $r$, 円周の長さを $l$ としたとき、
$$
\begin{align}
\pi = \frac{l}{2r} \\
l = 2\pi r
\end{align}
$$
となる。
度数法と弧度法の変換
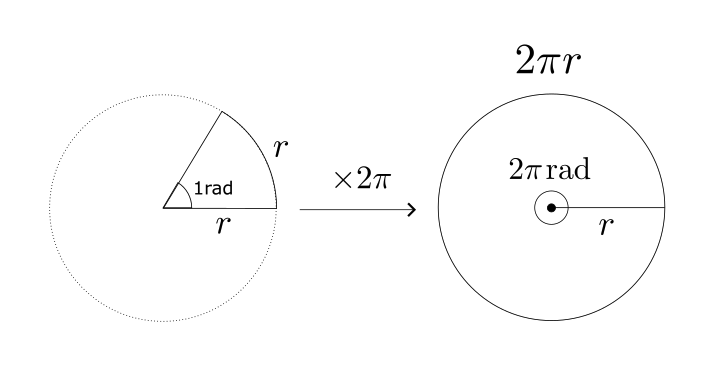
半径 $r$ としたとき、円周の長さは $2\pi r$ である。
円周の長さは中心角が1radである孤の長さより $2\pi$ 倍であるため、円周1週分の角度は $2\pi$ rad となる。
つまり、
$$
360^{\circ} = 2\pi\ \text{rad}
$$
このことから、
$$
1^{\circ} = \frac{\pi}{180}\ \mathrm{rad},\ 60^{\circ} = \frac{\pi}{3}\ \mathrm{rad},\ 225^{\circ} = \frac{5}{4}\pi\ \mathrm{rad}\ …
$$
となる。
また、単位「radian(rad)」はよく省略される。
例
例 1
$120^{\circ} = \frac{2}{3}\pi$ より
$$
\sin\frac{2}{3}\pi = \frac{\sqrt{3}}{2},\ \cos\frac{2}{3}\pi = -\frac{1}{2},\ \tan\frac{2}{3}\pi = -\sqrt{3}
$$
例 2
$390^{\circ} = \frac{13}{6}\pi$ の場合、図のような位置となる。
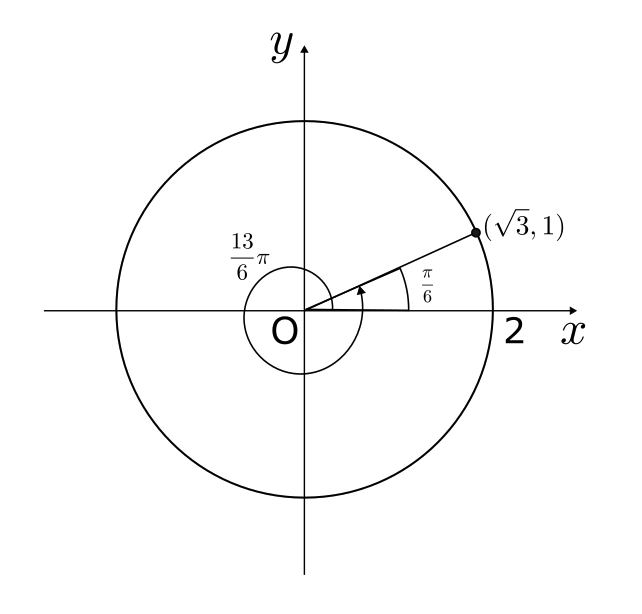
このとき、
$$
\begin{align}
\sin\frac{13}{6}\pi &= \sin\frac{\pi}{6} = \frac{1}{2} \\
\cos\frac{13}{6}\pi &= \cos\frac{\pi}{6} = \frac{\sqrt{3}}{2} \\
\tan\frac{13}{6}\pi &= \tan\frac{\pi}{6} = \frac{1}{\sqrt{3}}
\end{align}
$$
例 3
$\sin(-\frac{\pi}{4}),\ \cos(-\frac{\pi}{4}),\ \tan(-\frac{\pi}{4})$ を求める。$-\frac{\pi}{4}$ は図で表すと以下のような位置になる。
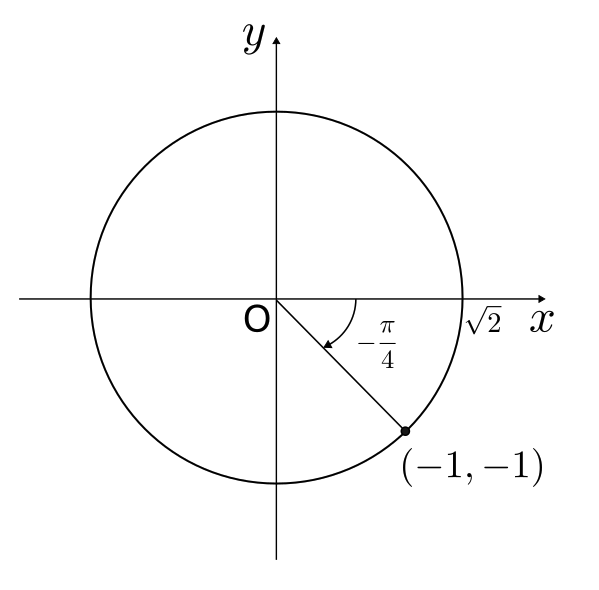
よって、
$$
\sin\left(-\frac{\pi}{4}\right) = -\frac{1}{\sqrt{2}},\ \cos\left(-\frac{\pi}{4}\right) = \frac{1}{\sqrt{2}}, \ \tan\left(-\frac{\pi}{4}\right) = -1
$$


