※ この記事はnoteをやっていた頃に投稿した記事です。こちらのブログに移しました。
note投稿時期
2023年1月27日
2023年2月5日
2023年2月23日
(元々noteではこの記事を3つに分けて投稿)
階乗
例えば、
$$1,2,3$$
を使って重複せずに3桁を作る方法は何通りあるだろうか?
考えらる方法を全て書き出すと、
123, 132, 213, 231, 312, 321
なので、答えは6通りである。
このように、場合の数は計算しなくても考えられる方法を全て書き出せば答えを導き出せることがいいところである。
でも、
$$1,2,3,4,5,6,7,8,9$$
を全て使って9桁作る方法は何通りあるか、という問題が出た場合、全て書いも求めることができるが気が遠くなってしまいそうだ。
そこで、階乗という計算方法を用いることでより楽に求めることができる。
まず初めに、
$$1,2$$
この二つの数字で2桁を作る方法は
12 と 21
の2通りである。
次に
$$1,2,3$$
で3桁を作る方法について考える。

例えば、
- 百の位が「1」のとき、残り二桁の並べ方は上でやった通り、2通り
- 百の位が「2」のとき、残り二桁の並べ方は上でやった通り、2通り
- 百の位が「3」のとき、残り二桁の並べ方は上でやった通り、2通り
となるので、3桁の作り方は
$$3\times 2 = 6通り$$
である。
さらに、
$$1,2,3,4$$
で4桁を作る方法について考える。
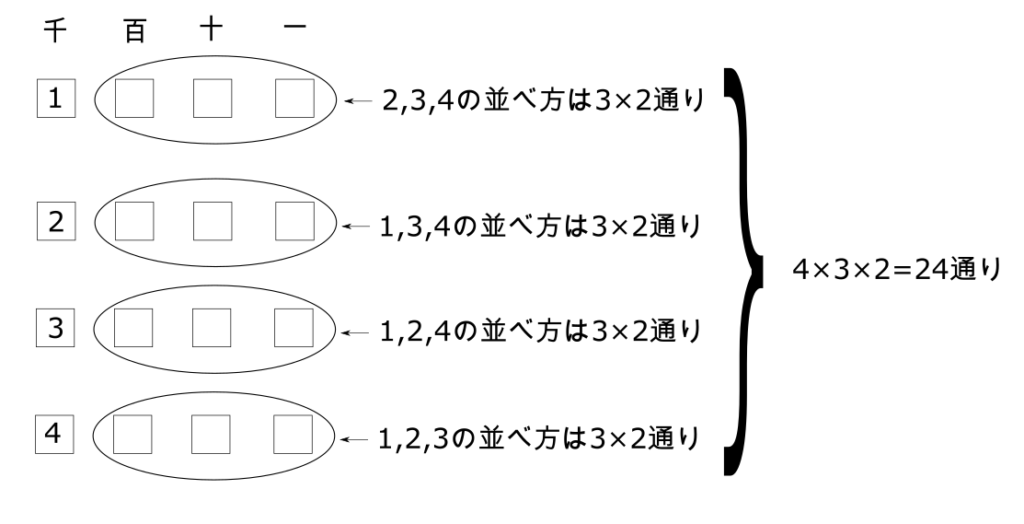
- 千の位が「1」のとき、残り3桁の並べ方は上でやった通り、3×2通り
- 千の位が「2」のとき、残り3桁の並べ方は上でやった通り、3×2通り
- 千の位が「3」のとき、残り3桁の並べ方は上でやった通り、3×2通り
- 千の位が「4」のとき、残り3桁の並べ方は上でやった通り、3×2通り
となるので、4桁の作り方は
$$4\times 3\times 2 = 24通り$$
である。
さらにさらに、
$$1,2,3,4,5$$
で5桁を作る方法について考える。
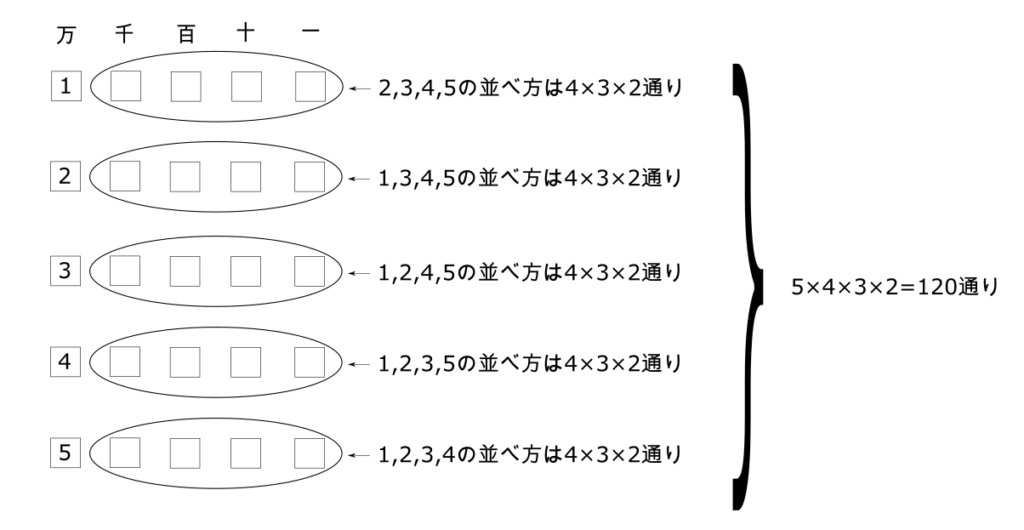
- 万の位が「1」のとき、残り4桁の並べ方は上でやった通り、4×3×2通り
- 万の位が「2」のとき、残り4桁の並べ方は上でやった通り、4×3×2通り
- 万の位が「3」のとき、残り4桁の並べ方は上でやった通り、4×3×2通り
- 万の位が「4」のとき、残り4桁の並べ方は上でやった通り、4×3×2通り
- 万の位が「5」のとき、残り4桁の並べ方は上でやった通り、4×3×2通り
となるので、5桁の作り方は
$$5\times 4\times 3\times 2 = 120通り$$
である。
ということは、
$$1,2,3,4,5.6$$
で6桁作る方法は
$$6\times 5\times 4\times 3\times 2 = 720通り$$
となるし、
$$1,2,3,4,5.6,7,8,9$$
で9桁を作る方法は
$$9\times 8\times 7\times 6\times 5\times 4\times 3\times 2 = 362880通り$$
となる。
また、
$$6\times 5\times 4\times 3\times 2\times 1$$
は「$6!$」と書き「6の階乗」、
$$9\times 8\times 7\times 6\times 5\times 4\times 3\times 2\times 1$$
は「$9!$」と書き「9の階乗」と読んだりする。
ということで、一般的に異なる$n$個の物を並び替える方法は
$$n! = n\times (n-1)\times (n-2)\times \cdots \times 2\times 1(通り)$$
となる。
今回はやらないが、ここで大事なのが、「異なる$n$個の・・・」の異なるである。
例えば、
$$1,1,1,2,3$$
のように、1が複数あって並び替える方法は別の求め方になる。
順列Pについて
こんな例を考えてみる。
$$1,2,3,4,5$$
この5つの数字の中から2つ選び2桁の数の作り方は何通りあるか考える。
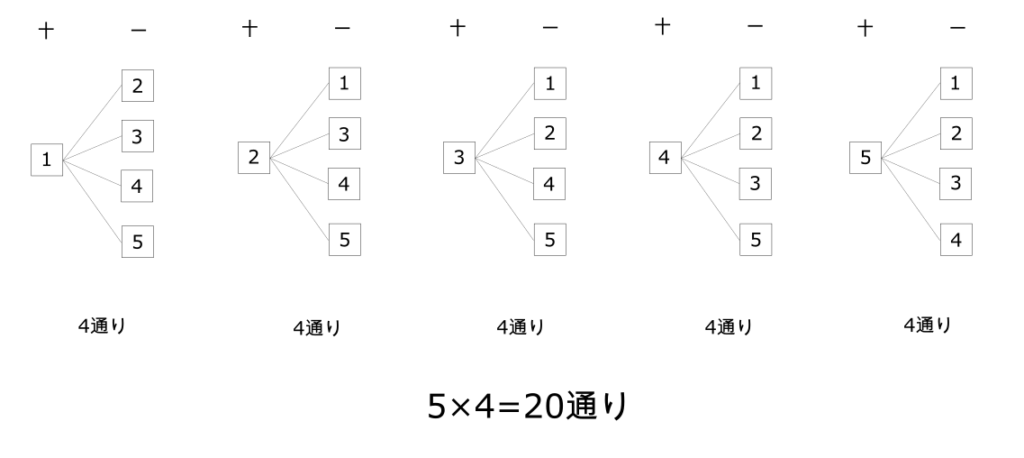
図のように、
- 十の位が1のとき、1の位は2,3,4,5の4通り
- 十の位が2のとき、1の位は1,3,4,5の4通り
- 十の位が3のとき、1の位は1,2,4,5の4通り
- 十の位が4のとき、1の位は1,2,3,5の4通り
- 十の位が5のとき、1の位は1,2,3,4の4通り
となるので、5つの数字の中から2つ選び2桁の数の作り方は
$$5\times 4 = 20通り$$
となる。
次に、5つの数字
$$1,2,3,4,5$$
の中から3つ選び3桁の数の作り方は何通りあるか考える。
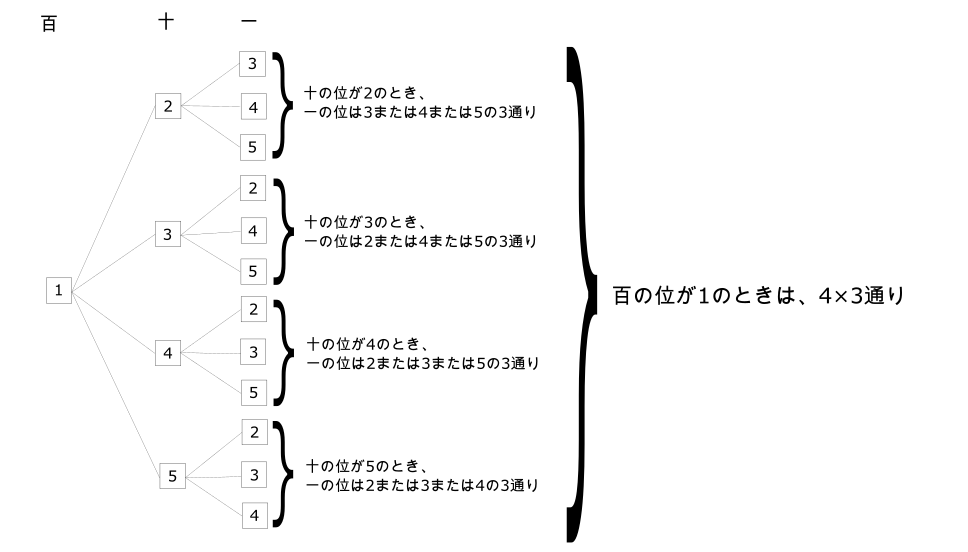
例えば、百の位が1のときを考える。
このとき、図のように
- 十の位が2のとき、1の位は3, 4, 5の3通り
- 十の位が3のとき、1の位は2, 4, 5の3通り
- 十の位が4のとき、1の位は2, 3, 5の3通り
- 十の位が5のとき、1の位は2, 3, 4の3通り
となるので、4×3=12通り
同様に、
- 百の位が2のとき、4×3=12通り
- 百の位が3のとき、4×3=12通り
- 百の位が4のとき、4×3=12通り
- 百の位が5のとき、4×3=12通り
となるので、3桁の作り方は
$$5\times 4\times 3 = 60通り$$
となる。
このように考えていくと、例えば
$$1,2,3,4,5,6,7,8,9$$
から4つ選び4桁の数字を作る方法は
$$9\times 8\times 7\times 6 = 3024通り$$
となる。
また、
$$9\times 8\times 7\times 6$$
は「P」を使って
$$_9P_4 = \underbrace{9\times 8\times 7\times 6}_{9から逆順に4つ掛ける}$$
表される。
他に、例えば$_{20}P_3$だと
$$_{20}P_3 = 20\times 19\times 18$$
と表される。
一般的に
$$_nP_r = \underbrace{n\times (n-1)\times \cdots \times (n – (r – 1))}_{r個}$$
であり、
異なる$n$個のものから$r$個取り出して並び替える方法は
$$_nP_r (通り)$$
である。
組み合わせCについて
以下のような例を考えてみる。
$$1,2,3,4,5$$
の中から2つの数を選ぶ方法は何通りあるか考えてみる。
まず、何通りあるか数えて求めてみると、
12, 13, 14, 15, 23, 24, 25, 34, 35, 45
の10通りである。
上で考えた順列の例と違うところは、選んだ後に並び替えないことである。
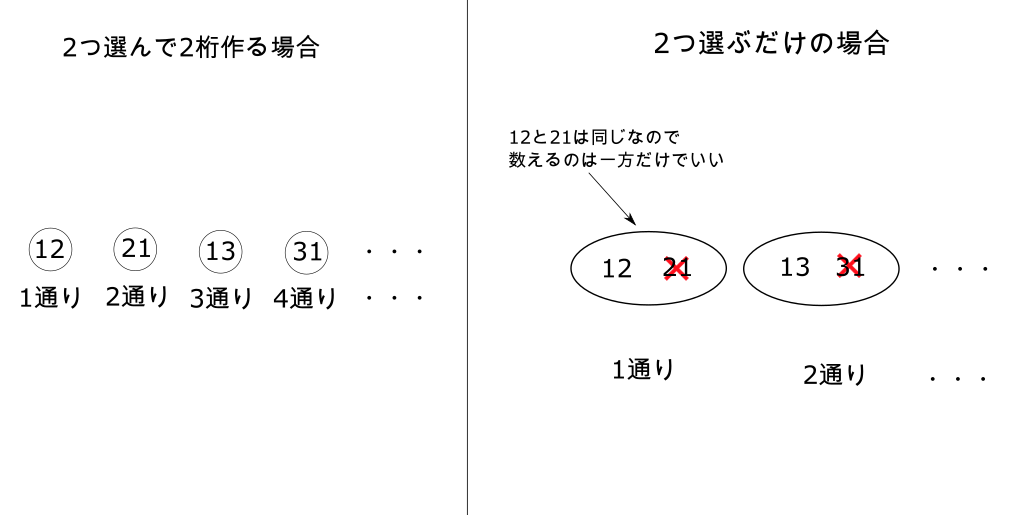
図のように、
選んで2桁を作る場合だと「12」と「21」は全く別物として数える。
しかし、今回は選んで並び替えなくていいので「12」と「21」は一括りで数える。
つまり、順列でやった「P」を用いた計算方法は数えなくてもいいものまで数えてしまうことになる。
では、どうやって求めるのか。

まず、5つの数字の中から2つ選んで並び替える方法は
$$_5P_2 = 5\times 4 = 20\ (通り)$$
だった。
この20個の2桁の数のうち「12」と「21」のように、取り出されている数が同じであるものは2つずつある。
なので、5つの数の中から2つ選ぶ方法は
$$20 \div 2 = 10\ (通り)$$
となる。
次に、
$$1,2,3,4,5$$
の中から3つ数を選ぶ方法について考えてみる。
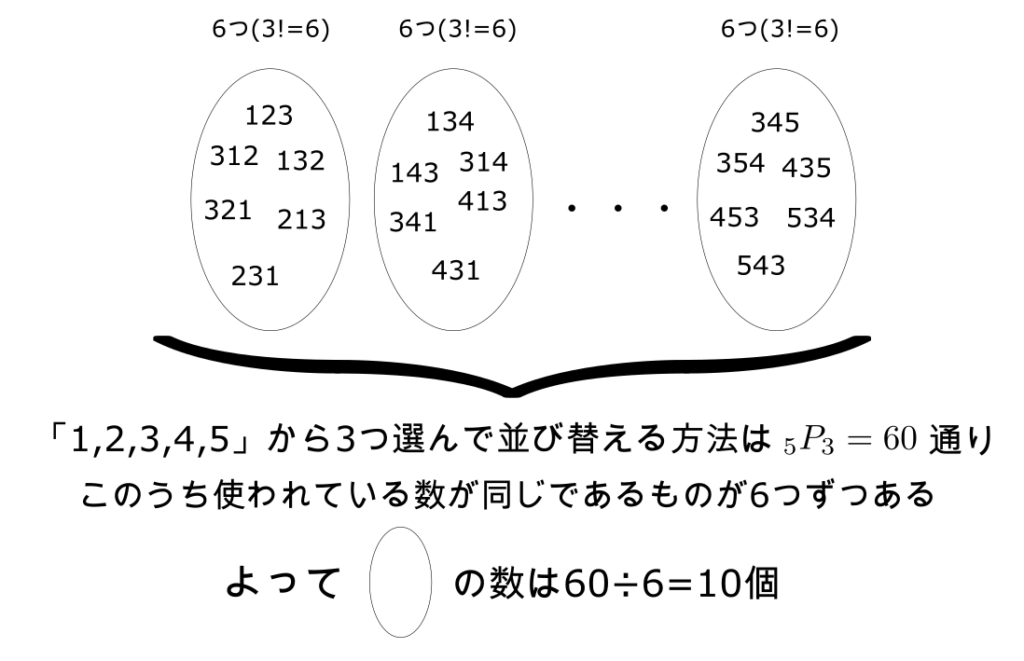
2つ選ぶ方法と同じようにまず、5つの数の中から3つ選んで並び替える方法は
$$_5P_3 = 60\ (通り)$$
である。
この60個の3桁の数のうち「123,132,…」のように、取り出されている数が同じであるものは6つずつある。
この「6」は異なる3つの数の並べ方が
$$3! = 6$$
であることから導き出すことができる。
なので、5つの数の中から3つ選ぶ方法は
$$60 \div 6 = 10\ (通り)$$
となる。
同様の求め方で次の例を考えてみる。
8つの数
$$1,2,3,4,5,6,7,8$$
の中から5つ選ぶ方法は何通りあるか求める。
まず、8つの数を選んで並び替える方法は
$$_8P_5 = 6720\ (通り)$$
この6720個の数のうち、取り出されている数が同じものは$5! = 120$個ずつある。(例えば、「12345」の場合は5つの数の並べ方なので、$5!$で求めることができる。)
よって、8つの数の中から5つ選ぶ方法は
$$_8P_5 \div 5! = 6720\div 120 = 56\ (通り)$$
となる。
また、
$$_8P_5 \div 5!$$
は「C」を使って、
$$_8C_5=_8P_5 \div 5! = \frac{8\times 7\times 6\times 5\times 4}{5\times 4\times 3\times 2\times 1}$$
と表される。
他に、$_{20}C_7$だと
$$_{20}C_7 = _{20}P_7 \div 7! = \frac{20\times 19\times 18\times 17\times 16\times 15\times 14}{7\times 6\times 5\times 4\times 3\times 2\times 1}$$
となる。
一般的に
$$_nC_r = \frac{_nP_r}{r!} = \frac{n\times (n-1)\times \cdots \times (n – (r – 1))}{r\times (r-1)\times \cdots \times 1}$$
であり、
異なる$n$個のものから$r$個選ぶ方法は
$$_nC_r\ (通り)$$
である。
まとめ
「P」と「C」の使い分け方は簡単にまとめると以下となる。

図のように取り出したものを区別して数える場合は「P」を使って計算する。
取り出したものを区別しないで数える場合は「C」を使って計算する。

