定義
$X$ と $Y$ を集合とする。
$X$ と $Y$ の直席集合 $X\times Y$ を
$$
X \times Y = \{(x,y)\mid x\in X, y\in Y\}
$$
と定義する。
さらに一般的に、$X_1, X_2, \cdots,X_n$ を集合とする。
このとき、$X_1\times X_2\times \cdots \times X_n$ を
$$
X_1\times X_2\times \cdots \times X_n = \{(x_1,x_2,\cdots,x_n)\mid x_1\in X_1,x_2\in X_2, \cdots , x_n\in X_n\}
$$
と定義する。
集合 $X$ に対して、$X$ の $n$ 個の直積 $\underbrace{X\times\cdots \times X}_{n個}$ を $X^n$ と書く。
例
例1
$X = \{1,2,3\}$, $Y = \{a,b\}$ とする。
このとき $X\times Y$ は
$$
X\times Y = \{(1,a), (1,b), (2,a), (2,b), (3,a), (3,b)\}
$$
となる。
例2
$X = \mathbb{Z}$ (整数全体の集合), $Y = \{a,b,\cdots,z\}$ (英小文字全体の集合)
このとき、$X\times Y$ は
$$
X\times Y = \{(\alpha,\beta)\mid \alpha\in \mathbb{Z}, \beta\in\{a,b,\cdots,z\}\}
$$
なので、
$$
X\times Y = \{(-1,b), (2000,z),(-1342, m),\cdots\}
$$
のような感じになる。
例3
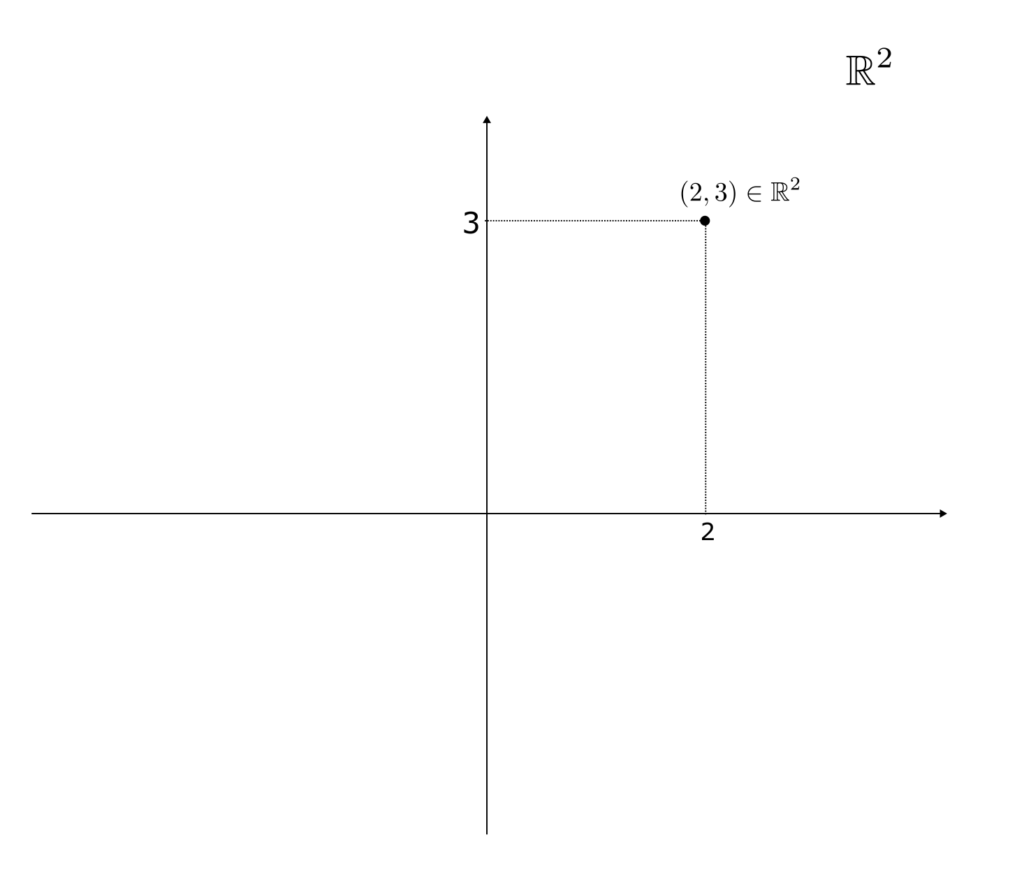
$$
\mathbb{R}^2 = \mathbb{R}\times\mathbb{R} = \{(x, y)\mid x,y\in\mathbb{R}\}
$$
これは、実数平面を表す集合でである。
例4
$$
\mathbb{R}\times \mathbb{Z} = \{(x,y)\mid x\in\mathbb{R},y\in\mathbb{Z}\}
$$
$\mathbb{R}\times \mathbb{Z}$ は $\mathbb{R}^2$ の部分集合であり、イメージとしては以下のようになる。


