定義(三角関数)
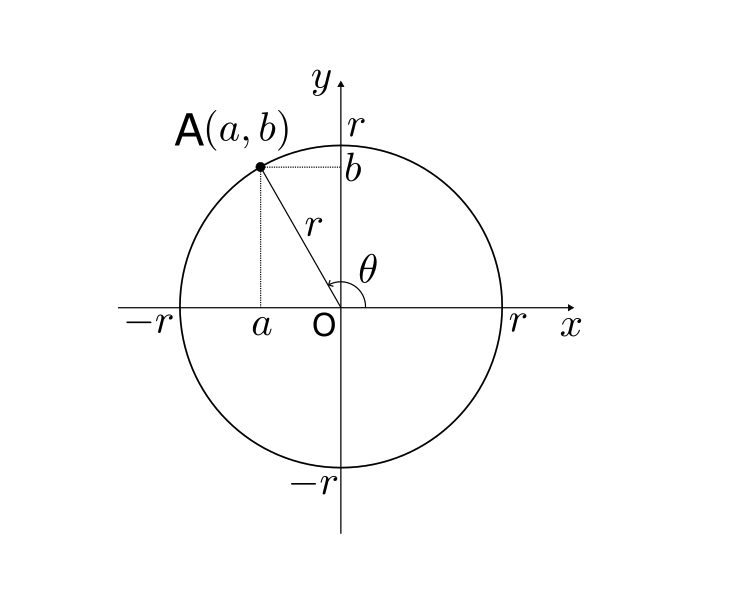
上記のように、半径 r の円を考える。反時計回りを正としてx 軸の正の部分から原点Oを中心に $\theta$ 回転させた円周上の点をA(a,b)とする。このとき、角 $\theta$ に対する正弦(sin), 余弦(cos), 正接(tan)は次のように定義する。
$$
\sin\theta = \frac{b}{r},\ \cos\theta = \frac{a}{r},\ \tan\theta = \frac{b}{a}
$$
例
例1
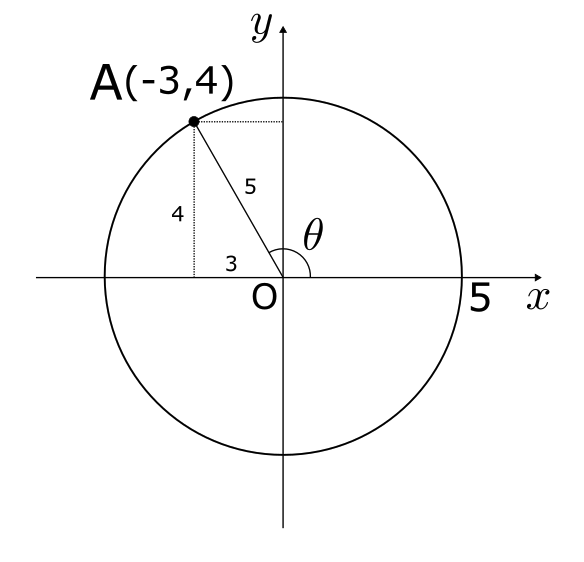
上記のように、点A \((-3, 4)\) をとる。三平方の定理より、\(OA = 5\) となる。反時計回りを正として、\(x\)軸と線分OAの角度を \(\theta\) とする。このとき、
$$
\sin\theta = \frac{4}{5},\ \cos\theta = -\frac{3}{5},\ \tan\theta = -\frac{4}{3}
$$
例2 (120°)
\(\theta = 120°\) のときのsin, cos, tanを求める。図のように、半径 2 の円を考える。このとき、点A \((-1, \sqrt{3})\) とすると、\(x\)軸と線分OAのなす角は120°となる。
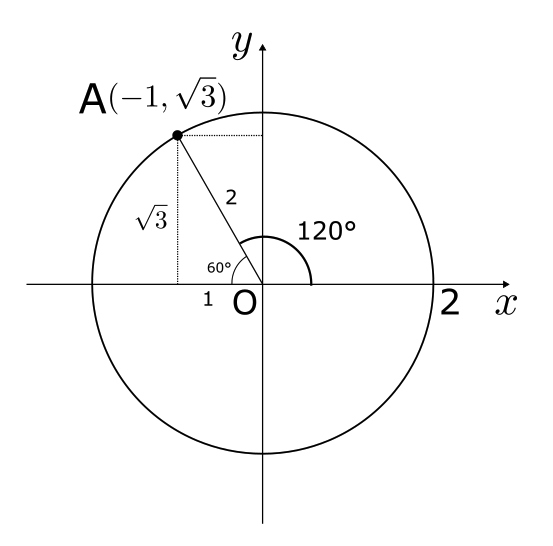
よって、
$$
\sin120°= \frac{\sqrt{3}}{2},\ \cos120°= -\frac{1}{2},\ \tan120°= -\sqrt{3}
$$
例3 (0°)
\(\theta = 0°\) のときのsin, cos, tanを求める。0°の場合は、半径1の円(単位円)を考え、 点Aは\((1,0)\) とすればいい。
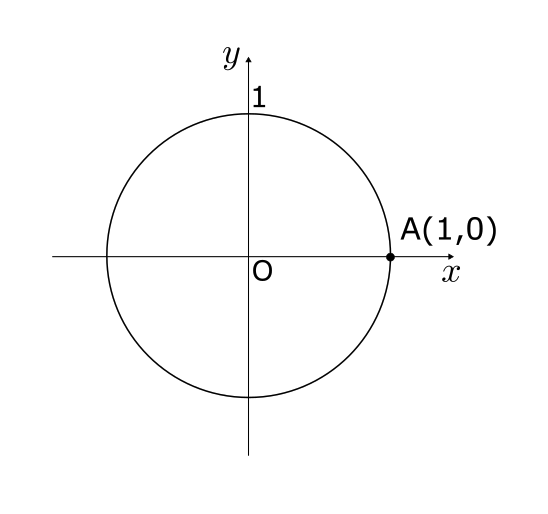
よって、
$$
\sin0°= \frac{0}{1} = 0,\
\cos0°= \frac{1}{1} = 1,\
\tan0°= \frac{0}{1} = 0
$$
となる。
例4 (270°)
\(\theta = 270°\) のときのsin, cos, tanを求める。図のように、半径 1 の円(単位円)を考える。このとき、円上の点Aを \((0,-1)\) とし、反時計回りを正とすると、\(x\)軸と線分OAのなす角は270°となる。
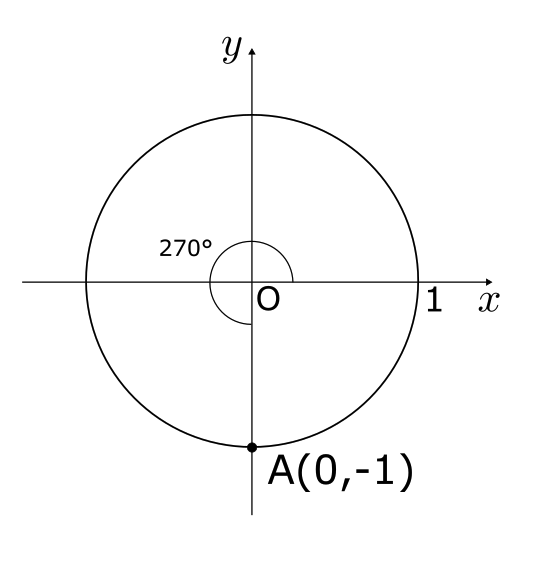
よって、
$$
\sin270° = -1,\ \cos270°= 0
$$
となる。\(\tan270°\)に関しては、定義に当てはめると、分母が0になってしまうため、存在しない。
まとめ
例のように三角関数を求めていくと以下のようになる。
| 0° | 30° | 45° | 60° | 90° | |
|---|---|---|---|---|---|
| sin(正弦) | 0 | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | 1 |
| cos(余弦) | 1 | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | 0 |
| tan(正接) | 0 | \(\frac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | / |
| 120° | 135° | 150° | 180° | |
|---|---|---|---|---|
| sin(正弦) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | 0 |
| cos(余弦) | \(-\frac{1}{2}\) | \(-\frac{1}{\sqrt{2}}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) |
| tan(正接) | \(-\sqrt{3}\) | \(-1\) | \(-\frac{1}{\sqrt{3}}\) | 0 |
| 210° | 225° | 240° | 270° | |
|---|---|---|---|---|
| sin(正弦) | \(-\frac{1}{2}\) | \(-\frac{1}{\sqrt{2}}\) | \(-\frac{\sqrt{3}}{2}\) | \(-1\) |
| cos(余弦) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{1}{\sqrt{2}}\) | \(-\frac{1}{2}\) | 1 |
| tan(正接) | \(\frac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | / |
| 300° | 315° | 330° | 360° | |
|---|---|---|---|---|
| sin(正弦) | \(-\frac{\sqrt{3}}{2}\) | \(-\frac{1}{\sqrt{2}}\) | \(-\frac{1}{2}\) | 0 |
| cos(余弦) | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | 1 |
| tan(正接) | \(-\sqrt{3}\) | \(-1\) | \(-\frac{1}{\sqrt{3}}\) | 0 |
補足
図1のような半径1と半径 \(r\) の円を考える。
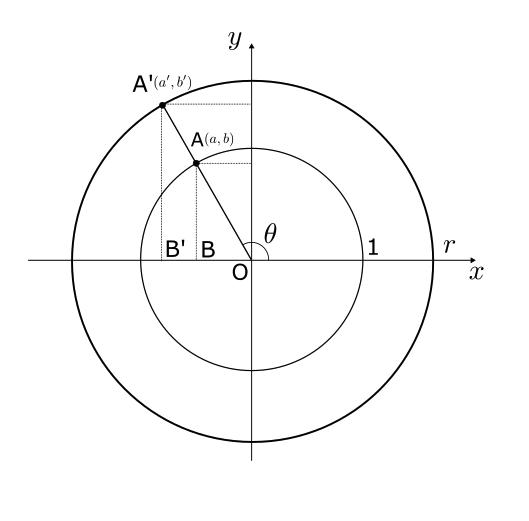
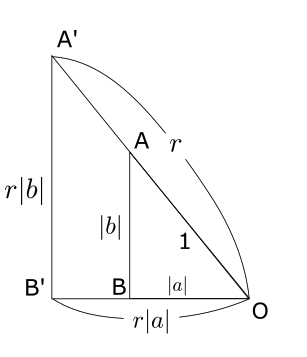
図1の△OABと△OA’B’は相似なので、\(a’ = ra,\ b’=rb\) となり、点A’は\((ra, rb)\) と書き直せる。(図2を参考)
半径1で考えたときの三角関数は
$$
\sin\theta = b,\ \cos\theta = a,\ \tan\theta = \frac{b}{a}
$$
半径 $r$ で考えたときの三角関数は
$$
\sin\theta = \frac{b’}{r} = \frac{rb}{r} = b, \
\cos\theta = \frac{a’}{r} = \frac{ra}{r} = a, \
\tan\theta = \frac{b’}{a’} = \frac{rb}{ra} = \frac{b}{a}
$$
となり半径1で考えたときと値が同じになる。つまり、三角関数を求める際、半径はどんな大きで考えても良い。


