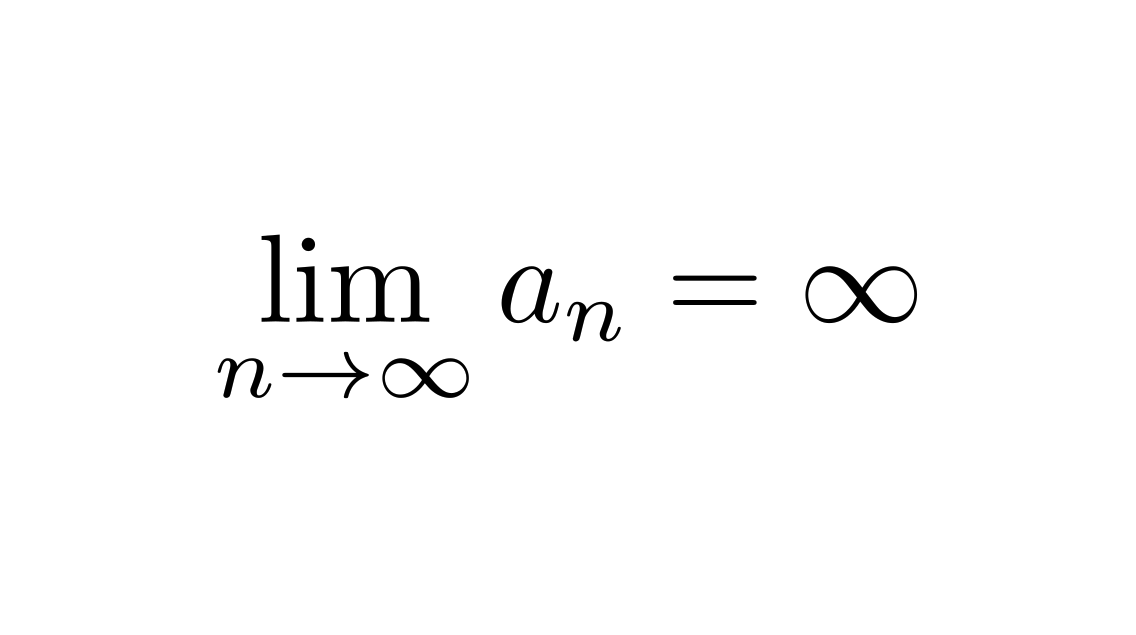前提知識
定義
数列 $\{a_n\}$ がどの値にも収束しないとき、数列 $\{a_n\}$ は発散するという。
例
$$
a_n = n \label{1}\tag{1}
$$
は発散する。
仮に、数列 $\{a_n\}$ が何かしらの値 $\alpha$ に収束したとする。すなわち、
$$
\lim_{n\to\infty}n = \alpha
$$
このとき、収束の定義を思い出してみると、どんな $\epsilon > 0$ を取ってきても十分大きな自然数 $n$ に対して、
$$
|n – \alpha|<\epsilon
$$
が成り立つはずである。
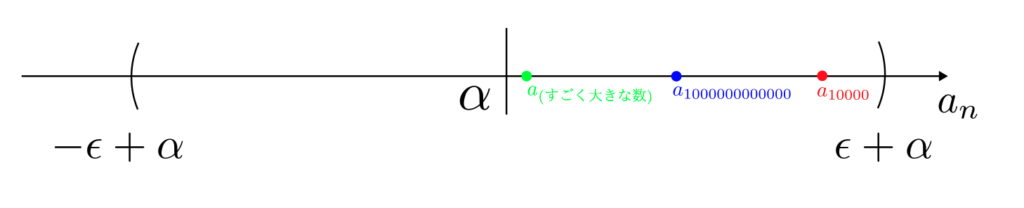
しかし、例えば $\epsilon = 1$ を取ってきたとする。
$$
N =
\begin{cases}
[\alpha] + 1 & (\alpha > 0)\\
1 & (\alpha \leq 0)
\end{cases}
$$
としたとき、$n\geq N$ を満たす任意の自然数 $n$ に対して、
$$
|n – \alpha| \geq 1
$$
になる。ただし、$[x]$ は $x$ を超えない最大の整数とする。(例えば、$[2.3]$ の場合 2.3 を超えない最大の整数は 2 なので、$[2.3] = 2$)
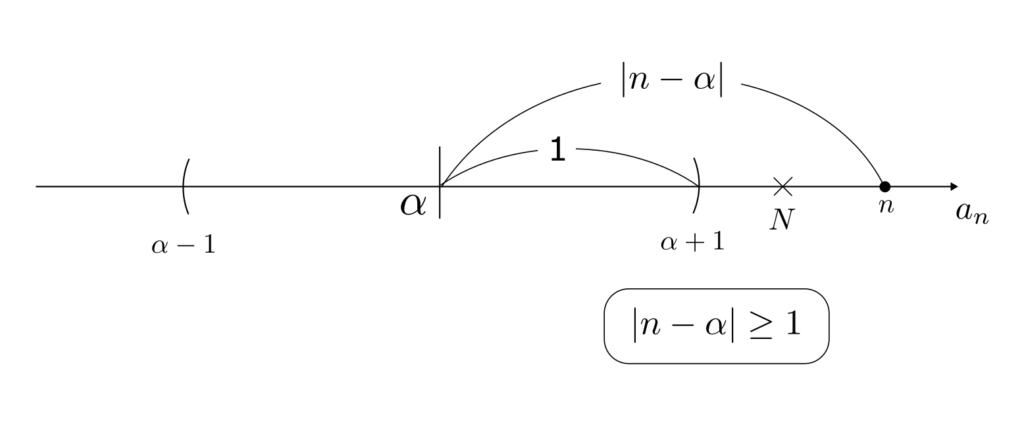
よって、どんな $\alpha$ を取ってきても、ある $\epsilon > 0$ に対しては、十分大きい$n$ に対して、$|n – \alpha| \geq \epsilon$ となってしまうため、$a_n = n$ は発散する。
発散の種類
$\infty$ に発散
上でやった例
$$
a_n = n
$$
は $n$ が十分大きくしていくと、$a_n$ も十分大きくなっていく。このとき、$\{a_n\}$ は $\infty$ に発散するといい、
$$
\lim_{n\to \infty} a_n = \infty
$$
と表す。
正確には、十分大きな正の実数 $M > 0$ を取ってきても、十分大きな自然数 $n$ に対して、$a_n > M$ が成り立つ、すなわち
任意の実数 $M > 0$ に対して、ある自然数 $N$ が存在して、$n\geq N$ を満たす任意の自然数 $n$ に対して、$a_n > M$
を満たすとき、数列 $\{a_n\}$ は $\infty$ に発散するという。
$a_n = n$ の場合、
$$
N = [M] + 1
$$
とおく事により、$\{a_n\}$ が $\infty$ に発散することが示せる。
$-\infty$ に発散
十分大きい自然数 $n$ に対して、 $a_n$ が負の方向に十分小さくなるとき 数列 $\{a_n\}$ は $-\infty$ に発散するといい、
$$
\lim_{n\to \infty} a_n = -\infty
$$
と書く。
簡単な例で言うと、$a_n = -n$ のとき $\{a_n\}$ は $-\infty$ に発散する。すなわち、
$$
\lim_{n\to \infty} (-n) = -\infty
$$
である。
正確な定義は、十分小さな実数 $M < 0$ を取ってきても、十分大きな自然数 $n$ に対して、$a_n < M$ が成り立つ、すなわち
任意の負の実数 $M < 0$ に対して、自然数 $N$ が存在し、$n \geq N$ を満たすすべての自然数 $n$ に対して、$a_n < M$
を満たすとき、$\{a_n\}$ は $-\infty$ に発散するという。
振動する
$\{a_n\}$ が収束せず、$\infty$ にも $-\infty$ にも発散しない場合、$\{a_n\}$ は振動すると言う。
例えば、
$$
a_n = (-1)^n
$$
の場合、数列 $\{a_n\}$ は発散するが、$\infty$ にも $-\infty$ にも発散しないので、この数列は振動する。
$\{a_n\}$ が発散することの理由
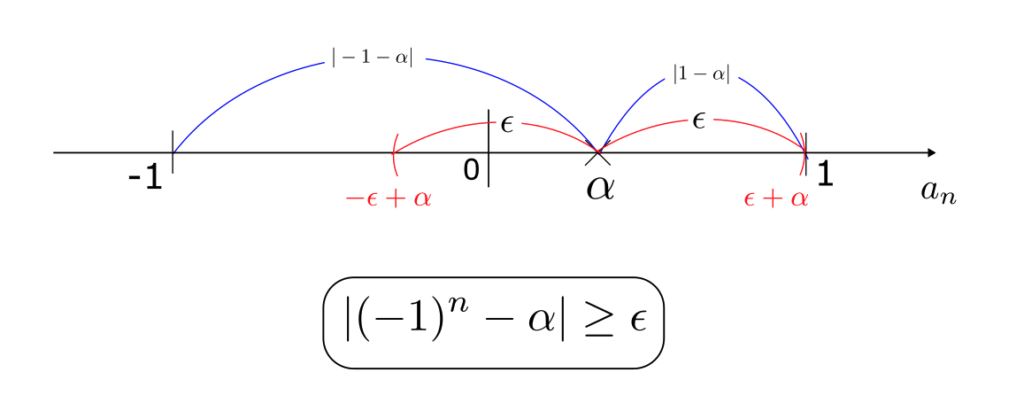
$a_1 = -1,\ a_2 = 1, \cdots,\ a_{2m-1}=-1,\ a_{2m} = 1$ のように、$a_n$ は $-1$ か 1 しか値を取らない。そのため、少なくとも $\{a_n\}$ は $-1$ や 1 に収束することはない。
例えば以下の図のような位置 $\alpha$ に収束するとする。

$\epsilon = |1 – \alpha|$ とすると、すべての自然数 $n$ に対して、
$$
|(-1)^n – \alpha|\geq \epsilon
$$
が成り立つ。
次に、$\{a_n\}$ は 1 にも収束しないこと確かめる。
$\epsilon = 1$ とする。$n$ が奇数のとき、$a_n = -1$ となるため、どんな自然数 $N$ を取ってきたとしても、$n$ が $n\geq N$ を満たす奇数のとき、$|(-1)^n – 1|\geq \epsilon$ となってしまう。
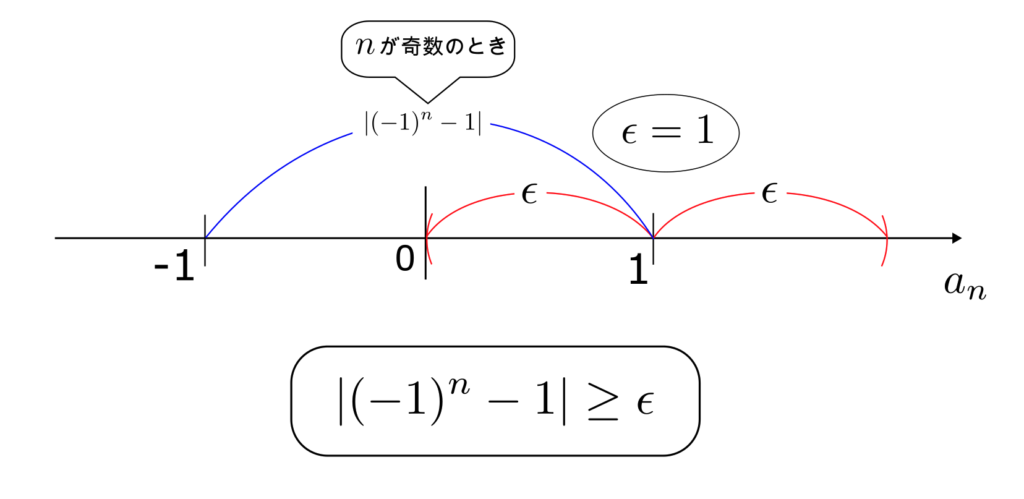
よって、$\{a_n\}$ は 1 には収束しない。
$\{a_n\}$ が $-1$ に収束しないことも同様の方法で示すことができる。
よって、$\{a_n\}$ は発散する。
$\{a_n\}$ が $\infty$ や $-\infty$ に発散しない理由
$M = 2$ のとき、すべての自然数 $n$ に対して、 $|(-1)^n| < M$ となるため、$\{a_n\}$ は $\infty$ に発散しない。
$M = -2$ のとき、すべての自然数 $n$ に対して、 $|(-1)^n| > M$ となるため、$\{a_n\}$ は $-\infty$ に発散しない。