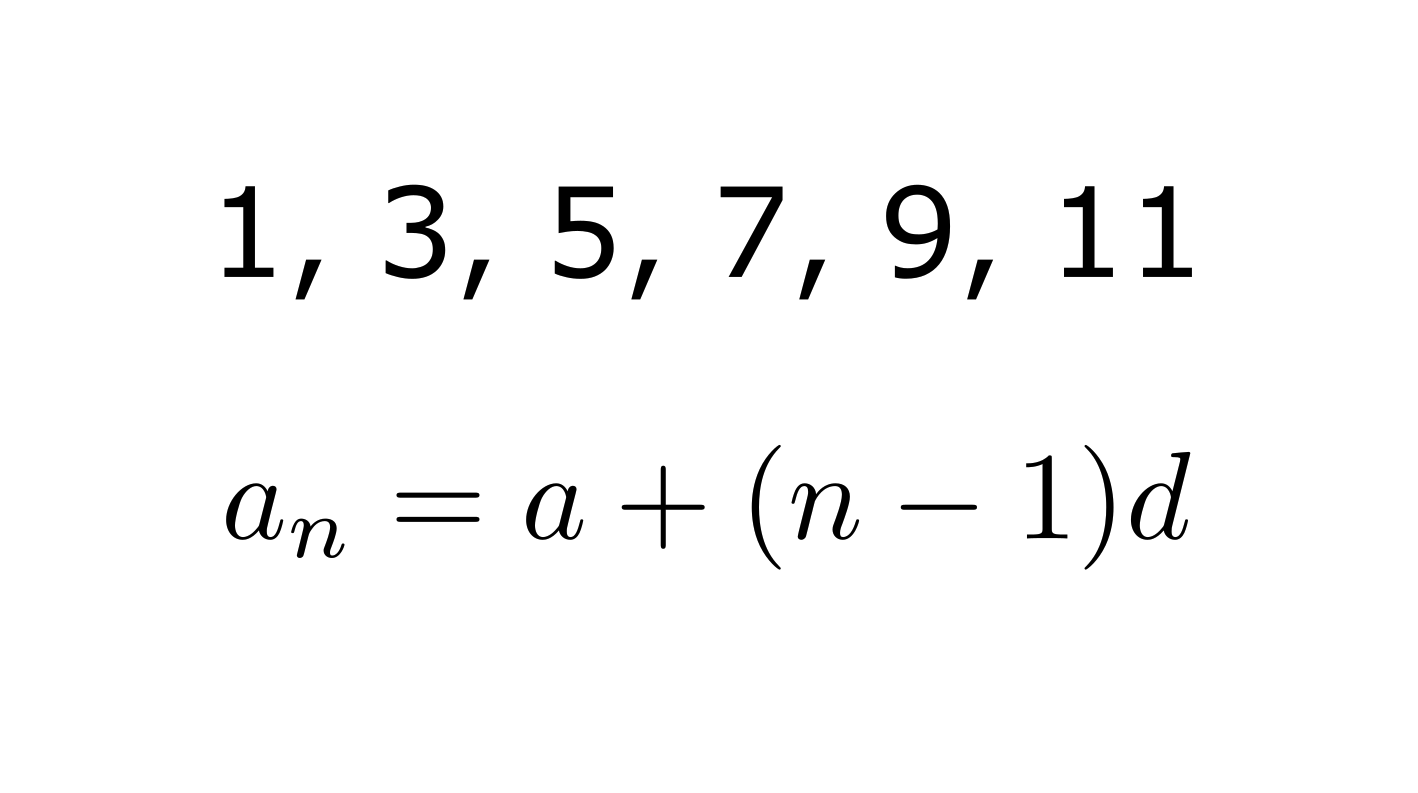数列とは
数を一列に並べたもの。
例えば、
4,2,5,7,4,1,7, …
である。一般的に文字を使って
$a_1, a_2, \cdots, a_n, \cdots$
と表す。
数列の1番最初の数 $a_1$ を初項、2, 3 番目の数 $a_2, a_3$ の数をそれぞれ第2項, 第3項と呼ぶ。
数列が有限であるとき、一番最後の項を末項と呼ぶ。
第 $n$ 項 $a_n$ を $n$ の式で表したものを一般項と呼ぶ。
数列の例
等差数列
2, 5, 8, 11, 14, …
上記のような初項 $a_1=2$ で $a_2 – a_1 = 3,\ a_3 – a_2 = 3, \cdots, a_{n+1} – a_n=3$ となる数列を考える。
この数列の一般項 $a_n$ は
$$
a_n = 3n-1
$$
である。
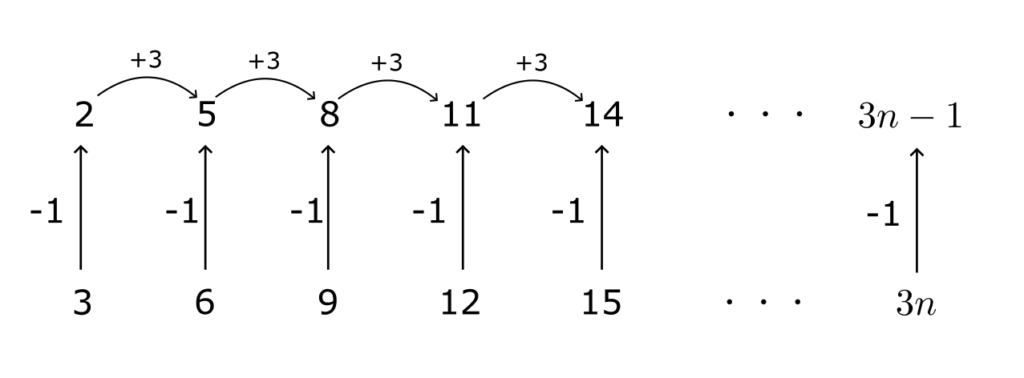
上記の例のように $a_{n+1} – a_{n} = (一定)$ であるような数列を等差数列と呼び、$a_{n+1} – a_{n}$ の値を公差と呼ぶ。
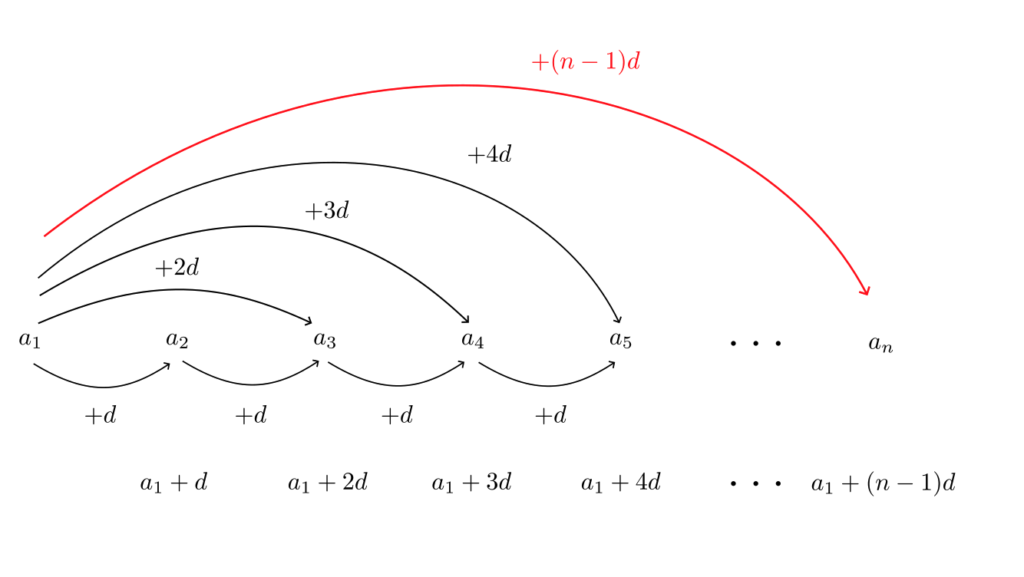
一般的に初項 $a_1$, 公差 $d$ の等差数列の一般項は
$$
a_n = a_1 + (n-1)d
$$
である。
等比数列
2, 6, 18, 54, 162, …
初項 $a_1 = 2$ で、$a_2/a_1 = 3,\ a_3/a_2 = 3, \cdots, a_{n+1}/a_n = 3$ となる数列を考える。
この数列の一般項 $a_n$ は
$$
a_n = 2 \cdot 3^{n-1}
$$
である。
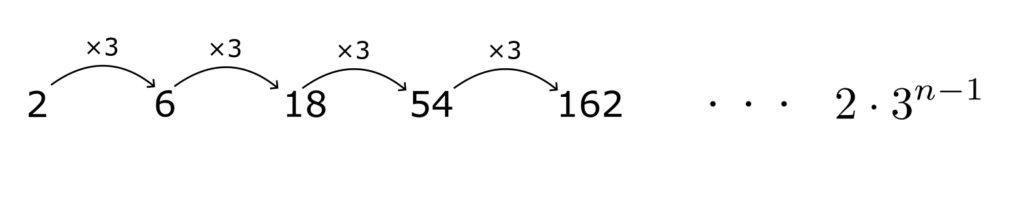
上記の例のように $a_{n+1}/a_{n} = (一定)$ であるような数列を等比数列と呼び、$a_{n+1}/a_{n}$ の値を公比と呼ぶ。
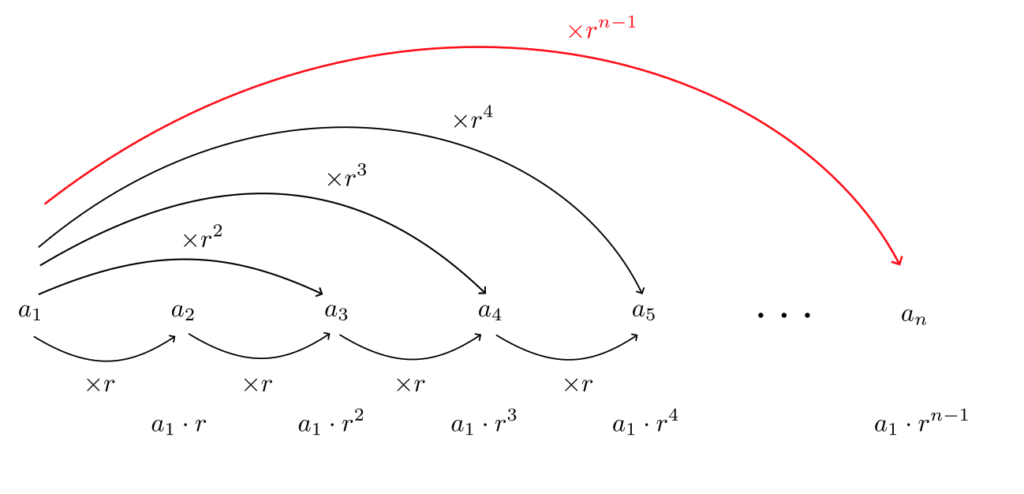
一般的に初項 $a_1$, 公比 $r$ の等比数列の一般項は
$$
a_n = a_1r^{n-1}
$$
である。