関連記事
平面ベクトルの成分表示
ベクトルでどの方向にどれくらいの大きさかを表す場合、ベクトルの成分表示を使って表現する。例えば、
$$
\vec{a} = (4,3)
$$
のように書く。これは、水平方向に4、垂直方向に3進めたベクトルである。
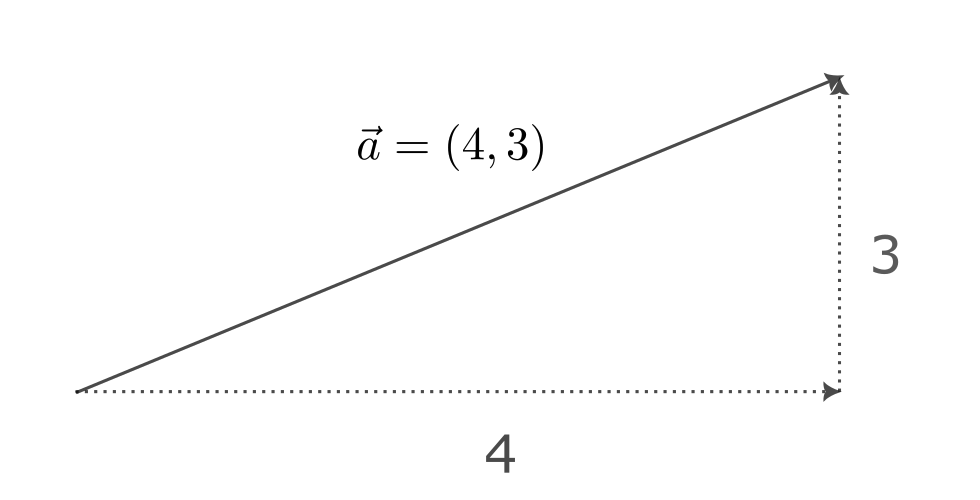
このベクトルの大きさは三平方の定理から
$$
|\vec{a}| = \sqrt{4^2 + 3^2} = 5
$$
である。
$\vec{a}$ の逆ベクトルは
$$
-\vec{a} = (-4, -3)
$$
である。
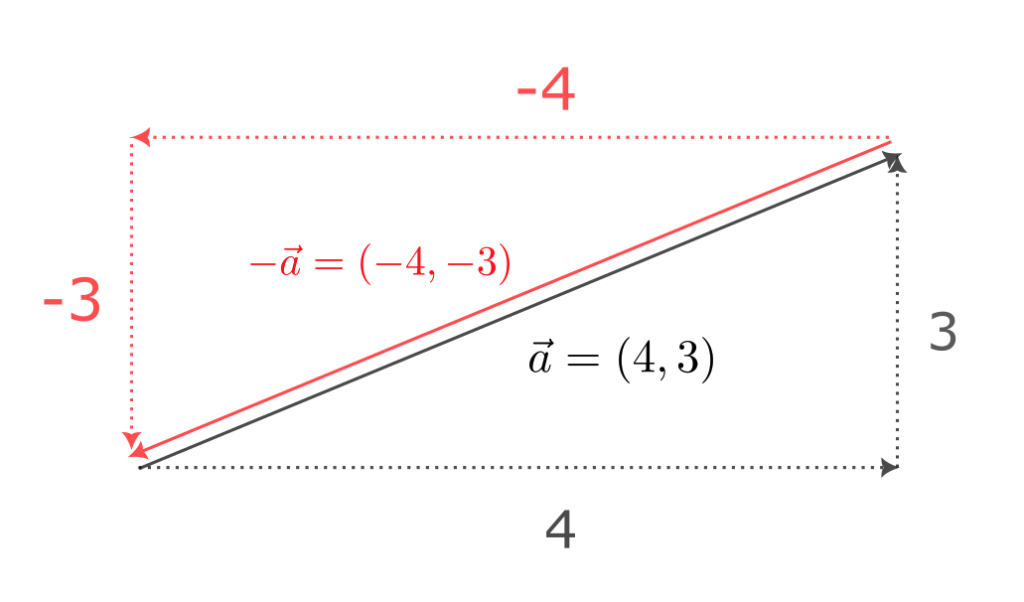
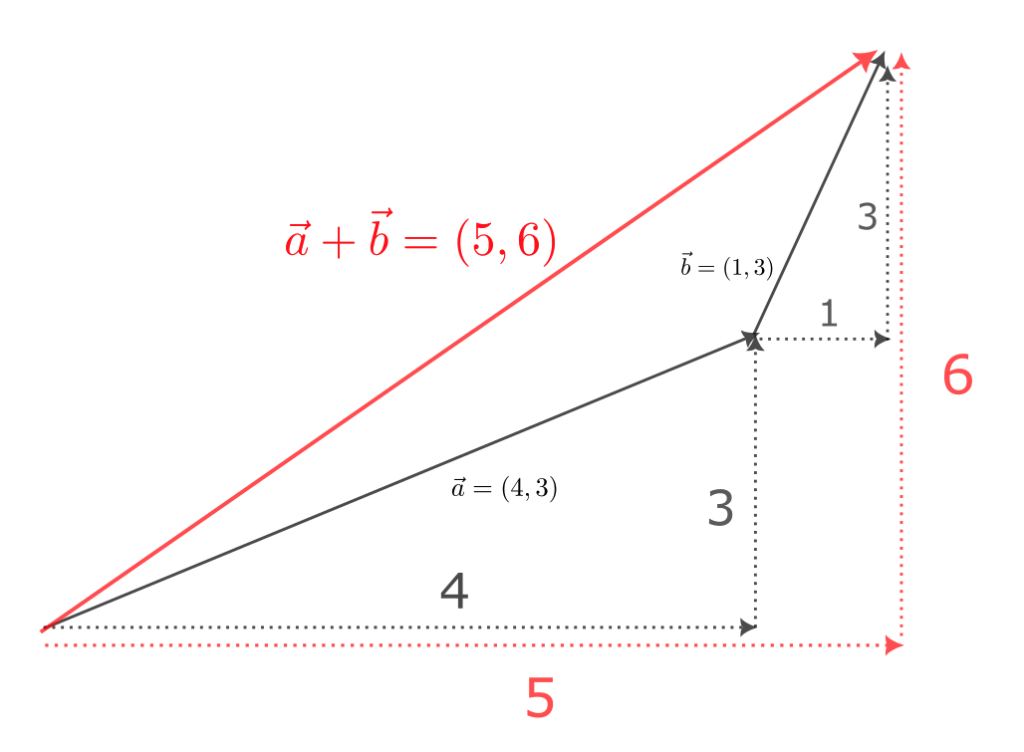
$\vec{b} = (1,3)$ とすると、
$$
\vec{a} + \vec{b} = (4 + 1, 3 + 3) = (5,6)
$$
となる。
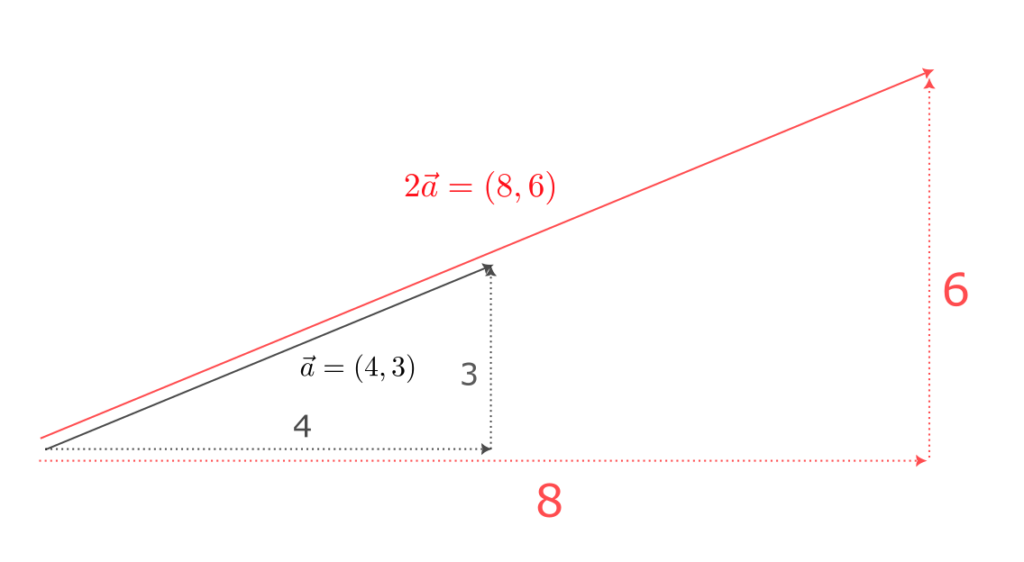
$\vec{c} = (8,6)$ とすると、$\vec{a}$ とは大きさは異なるが方向が同じベクトルであり、
$$
\vec{c} = 2\vec{a}
$$
と表すことができる。
平面ベクトルの1次独立
定義
以下を満たすとき、$\vec{a}$ と $\vec{b}$ は1次独立であるという。
$$
k\vec{a} + l\vec{b} = \vec{0} \Rightarrow k = l = 0
$$
例1
$$
\vec{a} = (2,1),\ \vec{b} = (1,3)
$$
$\vec{a}$ と $\vec{b}$ は1次独立である。
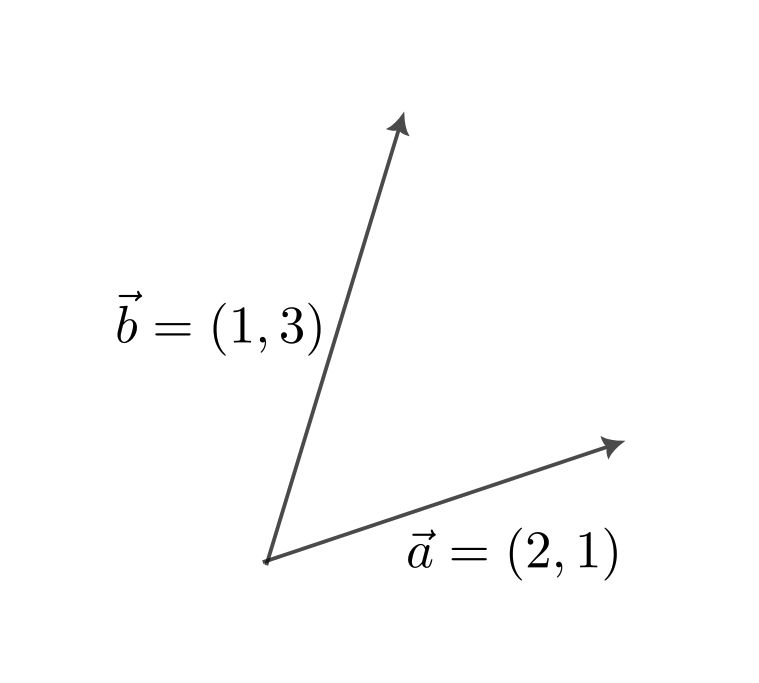
実際、
$$
k\vec{a} + l\vec{b} = (2k + l, k + 3l)
$$
である。$k\vec{a} + l\vec{b} = \vec{0}$ とすると
$$
\begin{cases}
2k + l = 0 \\
k + 3l = 0
\end{cases}
$$
である。よって、この方程式を解くと、$k = l = 0$ である。
例2
$$
\vec{a} = (1,2),\ \vec{b} = (2,4)
$$
とすると、$\vec{a}$ と $\vec{b}$ は1次独立でない。
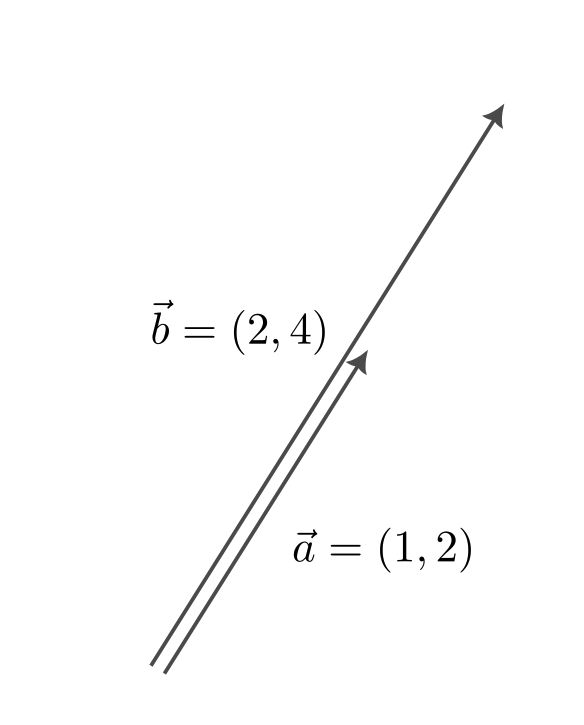
実際、$k\vec{a} + l\vec{b} = 0$ とすると、
$$
\begin{cases}
k + 2l = 0 \\
2k + 4l = 0
\end{cases}
$$
だが、$k=2,l=1$ は上記の方程式の解の1つである。
$k = l = 0$ 以外の解を持つため、$\vec{a}$ と $\vec{b}$ は1次独立でない。
1次独立の幾何学的性質
$\vec{a}$ と $\vec{b}$ が1次独立である$\Leftrightarrow$ $\vec{a}\neq \vec{0}$, $\vec{b}\neq 0$, $\vec{a}\nparallel\vec{b}$
証明
$\vec{a}$ と $\vec{b}$ が1次独立である$\Rightarrow$ $\vec{a}\neq \vec{0}$, $\vec{b}\neq 0$, $\vec{a}\nparallel\vec{b}$ を示す。
$\vec{a} = \vec{0}$ とする。例えば、$k = 1, l = 0$ としても、
$$
k\vec{a} + l\vec{b} = \vec{0}
$$
が成り立つため、$\vec{a}\neq \vec{0}$ である。
同じ理由で、$\vec{b} \neq \vec{0}$ である。
$\vec{a}\neq \vec{0}$, $\vec{b}\neq 0$, $\vec{a}\parallel\vec{b}$ とする。このとき、ある実数 $k$ に対して、
$$
\vec{b} = k\vec{a}
$$
と書くことができる。よって、
$$
k\vec{a} – \vec{b} = \vec{0}
$$
となり、$l\neq0$ でも $k\vec{a} + l\vec{b} = \vec{0}$ が成り立つため、$\vec{a}\nparallel\vec{b}$ でなければならない。
次に、$\vec{a}\neq \vec{0}$, $\vec{b}\neq 0$, $\vec{a}\nparallel\vec{b}$ $\Rightarrow$ $\vec{a}$ と $\vec{b}$ が1次独立であることを示す。
$k\vec{a} + l\vec{b} = \vec{0}$ とする。
仮に、$k\neq 0$ とすると、
$$
\vec{a} = -\frac{l}{k}\vec{b}
$$
となるが、これは $\vec{a}\parallel\vec{b}$ となるため矛盾する。よって、$k=0$である。
$l = 0$ も同様に示せる。
成分における性質
$\vec{a} = (a_1, a_2)$, $\vec{b} = (b_1, b_2)$ とする。
$\vec{a}$ と $\vec{b}$ は1次独立である $\Leftrightarrow$ $a_1b_2 – a_2b_1 \neq 0$ である。
証明
$$
k\vec{a} + l\vec{b} = (a_1k + b_1l, a_2k + b_2l)
$$
より、
$$
k\vec{a} + l\vec{b} = 0 \Leftrightarrow
\begin{cases}
a_1k + b_1l = 0 \\
a_2k + b_2l = 0
\end{cases}
\tag{1}\label{1}
$$
である。
$a_1b_2 – a_2b_1 \neq 0$ とする。
$(\ref{1})$ の連立方程式の上の式の両辺に $b_2$、下の式の両辺に $b_1$ をかけ、上の式から下の式を引くと
$$
(a_1b_2 – a_2b_1)k = 0
$$
となり、$a_1b_2 – a_2b_1 \neq 0$ より $k = 0$ となる。
$a_1b_2 – a_2b_1 \neq 0$ から $b_1 = b_2 = 0$ となることはないので、$(\ref{1})$ より $l=0$ がいえる。
よって、$\vec{a}$ と $\vec{b}$ は1次独立である。
逆に、$a_1b_2 – a_2b_1 = 0$ とすると、$\vec{a}$ と $\vec{b}$ は1次独立でないことを示す。
- $a_2 = 0$ とする。
このとき、$a_1b_2 = 0$ となるので、$a_1 = 0$ または $b_2 = 0$ である。
$a_1 = 0$ であれば、$\vec{a} = \vec{0}$ なので、$\vec{a}$ と $\vec{b}$ は1次独立ではない。
$b_2 = 0$ であれば、$\vec{a} = (a_1, 0), \vec{b} = (b_1, 0)$ となるため、 $\vec{a}$ と $\vec{b}$ は1次独立ではない。
- $a_2 \neq 0$ とする。
このとき、$a_1b_2 – a_2b_1 = 0$ から $b_1 = \frac{a_1b_2}{a_2}$ となる。これを $(\ref{1})$ の上の式に代入して整理すると、
$$
a_1a_2k + a_1b_2l = 0 \label{2}\tag{2}
$$
となる。
$a_1 = 0$ の場合、$a_1b_2 – a_2b_1 = 0$ より、$b_1 = 0$ となるが、$\vec{a} = (0, a_2), \vec{b} = (0, b_2)$ となるため、$\vec{a}$ と $\vec{b}$ は1次独立ではない。
$a_1 \neq 0$ の場合、$(\ref{2})$ は
$$
a_2k + b_2l = 0 \label{3}\tag{3}
$$
となり、$(\ref{1})$ の下の式と一致する。
$b_2 = 0$ の場合、$b_1 = 0$ となり、$\vec{b} = \vec{0}$ である。
$b_2 \neq 0$ の場合は $(\ref{3})$ は $k = l = 0$ 以外の解(例えば、$k = b_2, l = a_2$)を持つので、$\vec{a}$ と $\vec{b}$ は1次独立ではない。
以上から、$a_1b_2 – a_2b_1 = 0$ なら$\vec{a}$ と $\vec{b}$ は1次独立でないので、$\vec{a}$ と $\vec{b}$ は1次独立ならば$a_1b_2 – a_2b_1 \neq 0$ である。
平面ベクトルの性質
$\vec{a}$ と $\vec{b}$ は1次独立なベクトルとする。このとき、任意のベクトル $\vec{p}$ に対して、
$$
\vec{p} = k\vec{a} + l\vec{b}\ \ \ (k, l\text{ は実数})
$$
の形で表すことができる。

例
$$
\vec{a} = (2,1),\ \vec{b} = (1,3)
$$
とする。例えば、$\vec{p} = (3,2)$ とする。
$$
\vec{p} = k\vec{a} + l\vec{b}
$$
を満たす $k$ と $l$ の値は $k\vec{a} + l\vec{b} = (2k + l, k + 3l)$ なので、
$$
\begin{cases}
2k + l = 3 \\
k + 3l = 2
\end{cases}
$$
の解である。この方程式を解くと、$k = \frac{7}{5},\ l=\frac{1}{5}$ となる。よって、
$$
\vec{p} = \frac{7}{5}\vec{a} + \frac{1}{5}\vec{b}
$$
となる。
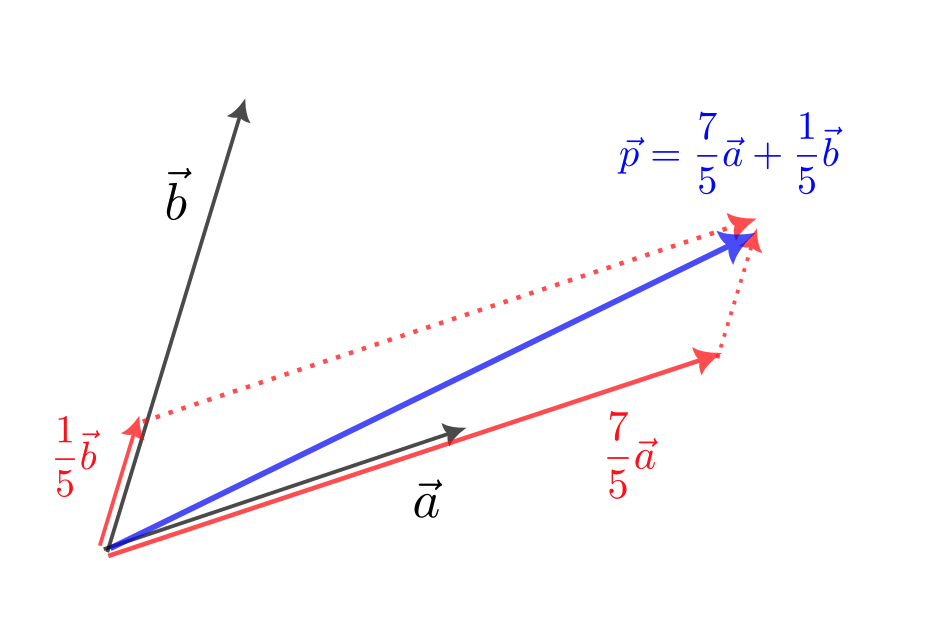
というような感じで、$\vec{a}$ と $\vec{b}$ が1次独立なら $\vec{a}$ のスカラー倍と $\vec{b}$ のスカラー倍の和によってどんなベクトルも作り出すことができる。
また、1次連立方程式の性質から任意の $\vec{p}$ に対して、
$$
\vec{p} = k\vec{a} + l\vec{b}
$$
を満たす $k,l$ はただ一つであるであることが感覚的に分かる。
まとめ
平面ベクトルにおいて、
ベクトル $\vec{a}$ と $\vec{b}$ は1次独立であることと、
任意のベクトル $\vec{p}$ に対して、
$$
\vec{p} = k\vec{a} + l\vec{b}
$$
を満たす $k, l$ が唯一つ存在することは同値である。
証明
$\vec{a} = (a_1, a_2), \vec{b} = (b_1,b_2)$ とする。
ベクトル $\vec{a}$ と $\vec{b}$ は1次独立であるとする。
任意のベクトル $\vec{p} = (p_1, p_2)$ をとる。
このとき、
$$
\vec{p} = k\vec{a} + l\vec{b} \Leftrightarrow
\begin{cases}
a_1k + b_1l = p_1 \\
a_2k + b_2l = p_2
\end{cases}
$$
である。$\vec{a}$ と $\vec{b}$ は1次独立である $\Rightarrow$ $a_1b_2 – a_2b_1 \neq 0$ よりこの連立方程式を解くと、
$$
k = \frac{p_1b_2 – b_1p_2}{a_1b_2 – b_1a_2},\ \ l = \frac{a_1p_2 – p_1a_2}{a_1b_2 – b_1a_2}
$$
となるため、$k,l$ の存在は示された。
$\vec{p}$ を $\vec{p} = k_1\vec{a} + l_1\vec{b}$ と $\vec{p} = k_2\vec{a} + l_2\vec{b}$ で表せたとする。$k_1\vec{a} + l_1\vec{b} = k_2\vec{a} + l_2\vec{b}$ より、$(k_1 – k_2)\vec{a} + (k_2 – l_2)\vec{b} = \vec{0}$ となる。
$\vec{a}$ と $\vec{b}$ は1次独立なので、$k_1 – k_2 = 0, l_1 – l_2 = 0$ 。よって、$k_1 = k_2, l_1 = l_2$ となるため、一意であることが示せた。
逆に、任意のベクトル $\vec{p}$ に対して、
$$
\vec{p} = k\vec{a} + l\vec{b} \label{4}\tag{4}
$$
を満たす $k, l$ が唯一つ存在するとする。
どんなベクトル $\vec{p}$ に対しても $(\ref{4})$ を満たす $k,l$ がただ一つ存在するので、$\vec{p} = \vec{0}$ としても$(\ref{4})$ を満たす $k,l$ がただ一つ存在する。$k = l = 0$ とすれば、$(\ref{4})$ は満たし、仮定からそれ以外の値を持たないため、$\vec{a}$ と $\vec{b}$ は1次独立である。
補足
ベクトル $\vec{p}$ に対して、$\vec{p} = k\vec{a} + l\vec{b}$ と表すことが出来るとき、$\vec{p}$ は $\vec{a}$ と $\vec{b}$ により生成されたベクトルと呼ぶことにする。
平面上の3つのベクトル $\vec{a}, \vec{b}, \vec{c}$ で考えてみる。
ベクトル $\vec{p}$ に対して、$\vec{p} = k\vec{a} + l\vec{b} + m\vec{c}$ と表すことが出来るとき、$\vec{p}$ は $\vec{a}$ と $\vec{b}$ と $\vec{c}$ により生成されたベクトルと呼ぶことにする。
$\vec{a}, \vec{b}, \vec{c}$ のうち2つが $\vec{0}$ や 3つとも並行であるとかでない限り、任意のベクトル $\vec{p}$ に対して、
$$
\vec{p} = k\vec{a} + l\vec{b} + m\vec{c}
$$
という形で表すことができる。
つまり平面上全てのベクトルは $\vec{a}$ と $\vec{b}$ と $\vec{c}$ により生成させることができる。
しかし、$\vec{p}$ の表し方はただ一つではない。($k,l,m$ はただ一つではない)
また、$\vec{a}, \vec{b}, \vec{c}$ が1次独立であるとは
$$
k\vec{a} + l\vec{b} + m\vec{c} = \vec{0} \Rightarrow k=l=m=0
$$
を満たすことであるが、平面の場合はどんなベクトルをとってきても、$\vec{a},\vec{b},\vec{c}$ は1次独立にならない。
1つのベクトルだけでは任意の平面上のベクトルを生成することはできない。
つまり、1次独立であり、任意のベクトルを生成させるために必要なベクトルは2つである。


