※ この記事はnoteをやっていた頃に投稿した記事です。こちらのブログに移しました。
(note投稿日:2022年8月27日)
最近ふと思った!
状況は以下の通り、、、
- 食器あらいしているとき、よくお箸を3膳まとめて洗う時がある。
- 洗った箸は目の前の棚に置いて乾かす。(箸の上には皿が乗っているので、箸の色などは見えない。)
- 次の食事の時に適当に箸を2本とる。

同じ種類の箸が取れない。。。
これの確率について考えてみる。
シンプルに考えてみる
赤色の箸と青色の箸と緑色の箸がそれぞれ1膳ずつあるとする。つまり、赤赤青青緑緑、の計6本。
例えば、この中無作為に箸2本選び、2本とも赤色の箸である確率は、
$$\frac{_2\mathrm{C}_2}{_6\mathrm{C}_2} = \frac{1}{15}$$
である。なので、無作為に2本選び、2本とも同じ色の箸である確率は
$$\frac{1}{15} \times 3 = \frac{1}{5}$$
である。
いや、ちょっと待てよ、、、
箸の取り方を思い返してみると、いつも隣同士の箸を選んでる。。。
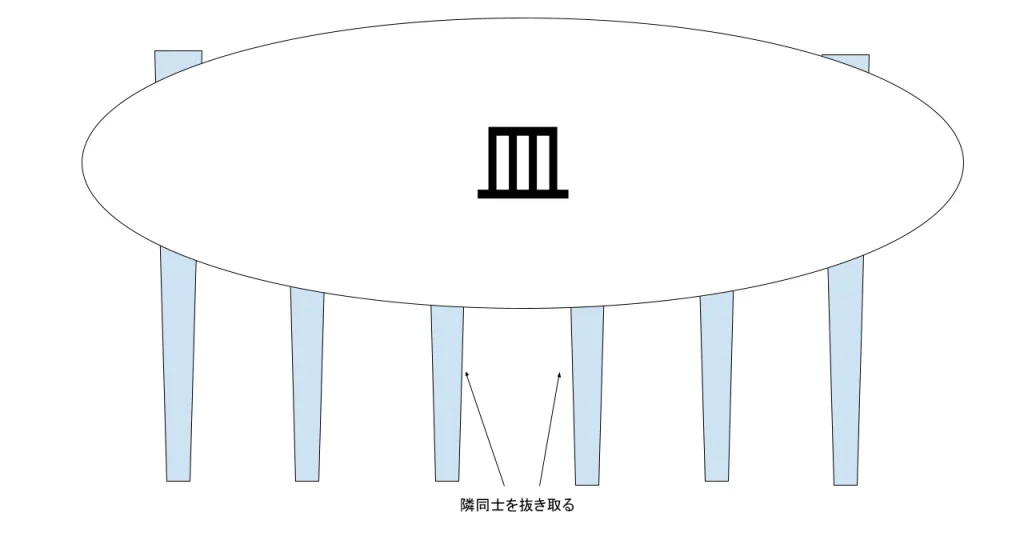
ということは、洗い物が終わり適当に箸を置いたときに、隣同士が異なる色(例えば、赤青緑赤青緑の順)だったら100%同じ色取れないやん!!
感覚的に確率下がるのでは、、、?
条件を少し加えてみる
無作為に箸を並べ、2本取り出すときは必ず隣同士の箸をとることにする。
まず、箸の並べ方は、
$$_6\mathrm{C}_2\cdot _4\mathrm{C}_2 = 90\ \mathrm{通り}$$
ある。
また、隣同士の箸を2本とる方法は5通りである。
これは、赤A, 赤B, 青A, 青B, 緑A, 緑Bと箸が並んでいたとすると取り方は
(赤A, 赤B), (赤B, 青A), (青A, 青B), (青B, 緑A), (緑A, 緑B)
次に、次の3つに場合分けして考えてみる。
- 赤赤青青緑緑のように、全ての箸が同じ色で隣り合っている
- 赤赤緑青青緑のように、2膳の箸が同じ色で隣り合っていて残りの1膳は隣り合っていない
- 赤赤青緑青緑のように、1膳の箸のみが同じ色で隣り合っている
- 1の場合
全て書くと、
赤赤青青緑緑, 赤赤緑緑青青, 青青赤赤緑緑, 青青緑緑赤赤, 緑緑赤赤青青, 緑緑青青赤赤
の6通り。
また、例えば「赤赤青青緑緑」の並びで、隣同士の箸を抜いたときに同じ色である確率は$\frac{3}{5}$である。
なので、1の場合隣同士の箸を抜いたときに同じ色である確率は
$$\frac{6}{90}\times \frac{3}{5} = \frac{18}{450}$$
- 2の場合
赤同士、青同士が隣り合っていて、緑は隣り合っていない場合を全て書くと
赤赤緑青青緑, 青青緑赤赤緑, 緑赤赤青青緑, 緑青青赤赤緑, 緑赤赤緑青青, 緑青青緑赤赤
の6通り。なので、2膳の箸が同じ色で隣り合っていて残りの1膳は隣り合っていない場合は$6\times 3 = 18$通り。
また、例えば「赤赤緑青青緑」の並びで、隣同士の箸を抜いたときに同じ色である確率は$\frac{2}{5}$である。
なので、2の場合隣同士の箸を抜いたときに同じ色である確率は
$$\frac{18}{90}\times \frac{2}{5} = \frac{36}{450}$$
- 3の場合
赤のみ隣り合っている場合を全て書くと、
赤赤青緑青緑, 赤赤緑青緑青, 青赤赤緑青緑, 緑赤赤青緑青, 青緑赤赤青緑, 青緑赤赤緑青, 緑青赤赤青緑, 緑青赤赤緑青, 青緑青赤赤緑, 緑青緑赤赤青, 青緑青緑赤赤, 緑青緑青赤赤
の12通り。なので、1膳の箸のみが同じ色で隣り合っている場合は$12\times 3 = 36$通り。
また、例えば「赤赤青緑青緑」の並びで、隣同士の箸を抜いたときに同じ色である確率は$\frac{1}{5}$である。
なので、3の場合隣同士の箸を抜いたときに同じ色である確率は
$$\frac{36}{90}\times \frac{1}{5} = \frac{36}{450}$$
よって、以上のことから、
$$\frac{18}{450} + \frac{36}{450} + \frac{36}{450} = \frac{1}{5}$$
シンプルに考えた時と確率が同じになった!!!


