事前知識
例1 $(\frac{\pi}{2} – \theta)$ の三角関数
$0 < \theta < \frac{\pi}{2}$ とする。
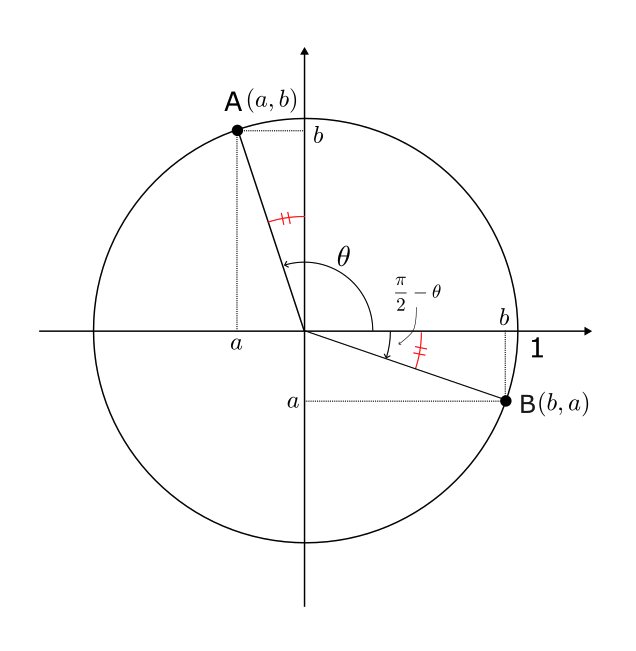
例えば、半径1の円(単位円) を考えたとき、$\theta$ が以下の図のような位置にあったとする。
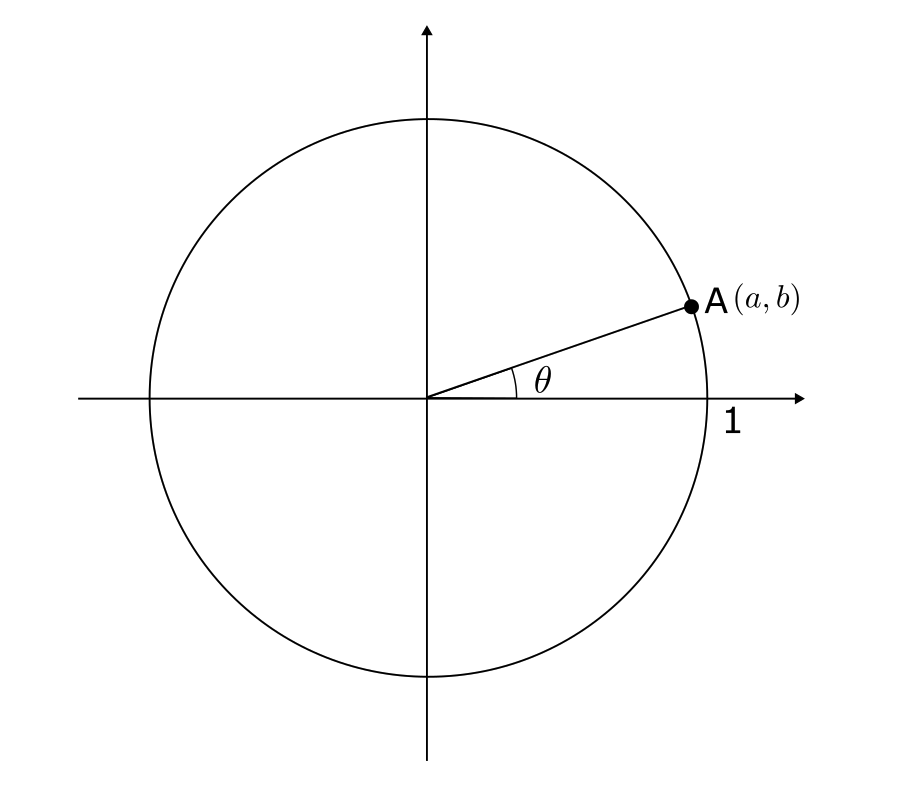
図のように、点Aの座標を $(a,b)$ としたとき、
$$
\sin\theta = b, \cos\theta = a, \tan\theta = \frac{b}{a} \label{1}\tag{1}
$$
である。
$(\frac{\pi}{2} – \theta)$ は以下の図のような位置にある。
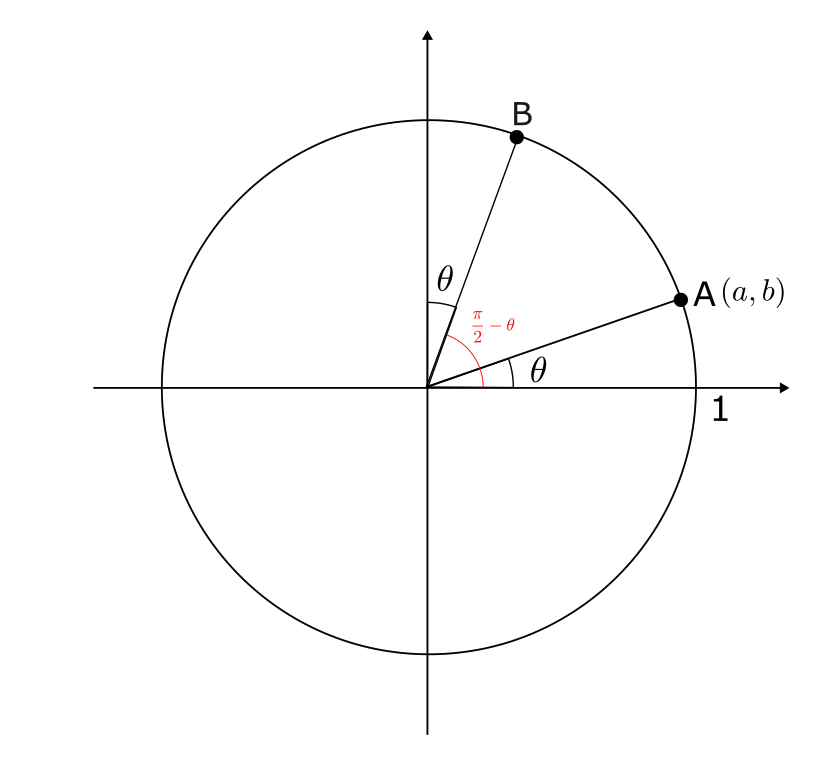
このとき、点Bは $(b, a)$ になる。
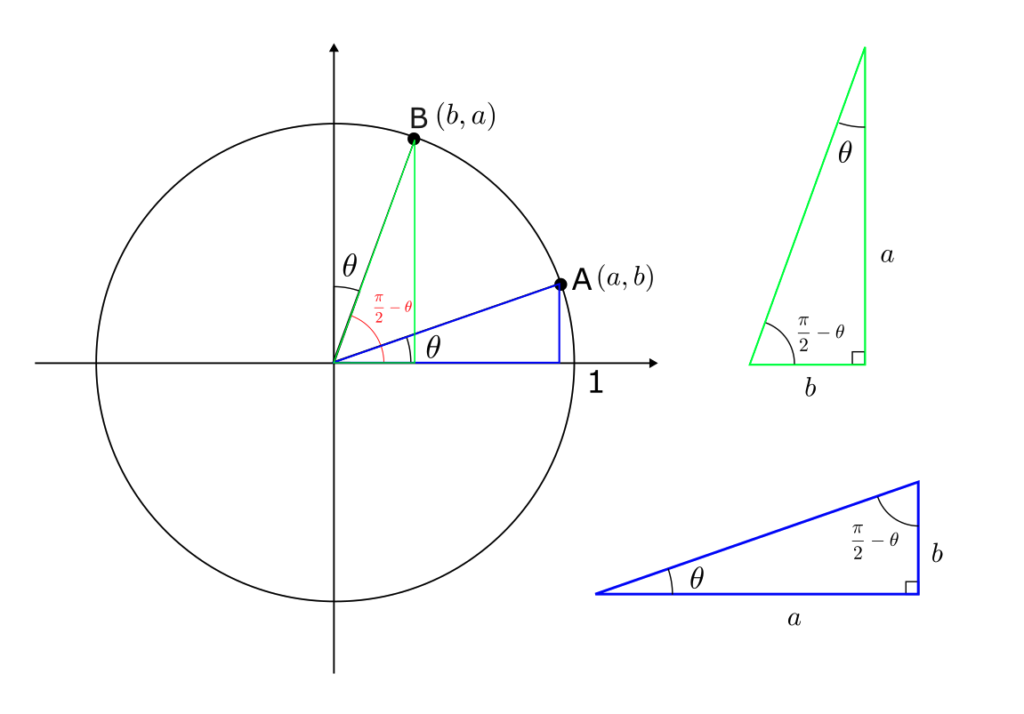
よって、
$$
\sin\left(\frac{\pi}{2} – \theta\right) = b,\
\cos\left(\frac{\pi}{2} – \theta\right) = a,\
\tan\left(\frac{\pi}{2} – \theta\right) = \frac{a}{b} \label{2}\tag{2}
$$
となる。
$(\ref{1})$ と $(\ref{2})$ を比較することにより、
$$
\sin\left(\frac{\pi}{2} – \theta\right) = \cos\theta,\
\cos\left(\frac{\pi}{2} – \theta\right) = \sin\theta.\
\tan\left(\frac{\pi}{2} – \theta\right) = \frac{1}{\tan\theta} \label{3}\tag{3}
$$
となる。
簡単なため、$0 < \theta < \frac{\pi}{2}$ で考えたが、それ以外の角度でも同じ結果となる。
例えば、$\theta$ が以下の位置にあるとする。
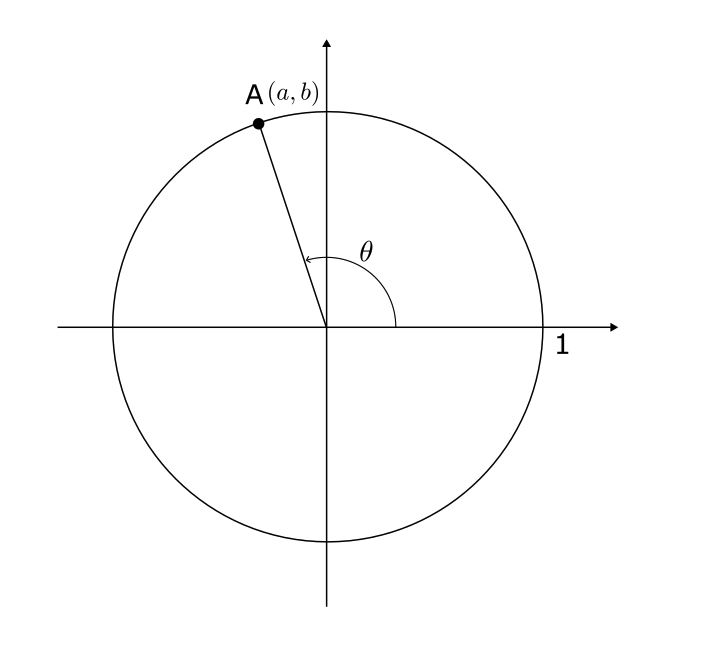
このとき、$(\frac{\pi}{2} – \theta)$ は以下の図のような位置にある。
点Aを$(a, b)$とすると、点Bは$(b,a)$なり、$(\ref{3})$ と同じ結果になる。
例2 $(\pi – \theta)$ の三角関数
$\theta$が以下の 以下の図のような位置にあったとする。

このとき、$(\pi – \theta)$ は以下の図のような位置にある。
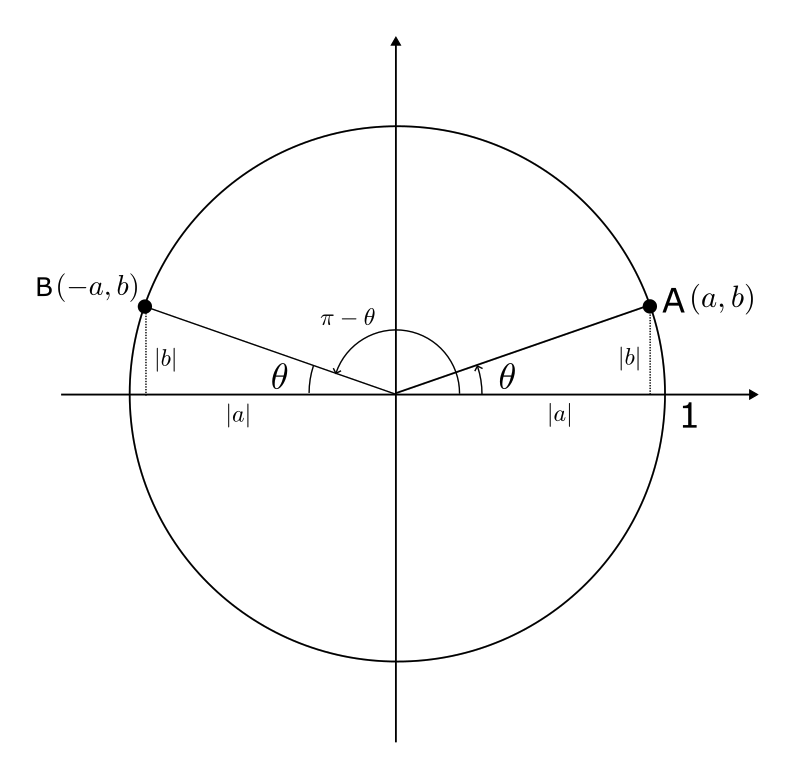
点Aを$(a, b)$とすると、点Bは$(-a,b)$となる。
よって、
$$
\sin\theta = b,\ \cos\theta = a,\ \tan\theta = \frac{b}{a} \label{4}\tag{4}
$$
$$
\sin(\pi – \theta) = b,\ \cos(\pi – \theta) = -a,\ \tan(\pi – \theta) = -\frac{b}{a} \label{5}\tag{5}
$$
となる。$(\ref{4})$と$(\ref{5})$を比較することにより、
$$
\sin(\pi – \theta) = \sin\theta,\
\cos(\pi – \theta) = -\cos\theta,\
\tan(\pi – \theta) = -\tan\theta
$$
でとなる。
まとめ
例1, 例2のように考えていくと以下のようなことが言える。
$$
\sin\left(\frac{\pi}{2} – \theta\right) = \cos\theta,\
\cos\left(\frac{\pi}{2} – \theta\right) = \sin\theta.\
\tan\left(\frac{\pi}{2} – \theta\right) = \frac{1}{\tan\theta}
$$
$$
\sin\left(\frac{\pi}{2} + \theta\right) = \cos\theta,\
\cos\left(\frac{\pi}{2} + \theta\right) = -\sin\theta.\
\tan\left(\frac{\pi}{2} + \theta\right) = -\frac{1}{\tan\theta}
$$
$$
\sin(\pi – \theta) = \sin\theta,\
\cos(\pi – \theta) = -\cos\theta,\
\tan(\pi – \theta) = -\tan\theta
$$
$$
\sin(\pi + \theta) = -\sin\theta,\
\cos(\pi + \theta) = -\cos\theta,\
\tan(\pi + \theta) = \tan\theta
$$
$$
\sin\left(\frac{3}{2}\pi – \theta\right) = -\cos\theta,\
\cos\left(\frac{3}{2}\pi – \theta\right) = -\sin\theta.\
\tan\left(\frac{3}{2}\pi – \theta\right) = \frac{1}{\tan\theta}
$$
$$
\sin\left(\frac{3}{2}\pi + \theta\right) = -\cos\theta,\
\cos\left(\frac{3}{2}\pi + \theta\right) = \sin\theta.\
\tan\left(\frac{3}{2}\pi + \theta\right) = -\frac{1}{\tan\theta}
$$
$$
\sin(-\theta) = -\sin\theta,\
\cos(-\theta) = \cos\theta,\
\tan(- \theta) = -\tan\theta
$$


