イントロダクション
Pythonで第一四分位数や第三四分位数を出力する方法を調べていると、statisitcs を使う方法と NumPy を使う方法を見つけた。
statistics を使う場合:
statistics.quantiles(data)で第一四分位数、第二四分位数(中央値)、第三四分位数を求めることができる。
NumPy を使う場合:
np.percentile(data, 25)または
np.quantile(data, 0.25)で 第一四分位数を求めることができる。
例えば、dataを
[26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
とする。
statistics の場合:
import statistics
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
print(statistics.quantiles(data))とすると、
# [第一四分位数, 第二四分位数, 第三分位数]
[12.0, 20.0, 30.0]と出力される。
NumPy の場合:
import numpy as np
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
print(np.percentile(data, 25))とすると、
12.5と出力される。
statistics を使った場合と NumPy を使った場合とで同じ第一四分位数でも結果が異なった。
そこで、statistics と NumPy での分位数の計算方法を調べてみた。
numpy.percentile
ドキュメントを見ると、分位数を求める際の分割方法が9つに分かれている。1(他プラス4つの方法も記載されているが、後方互換性のために保持されているらしい。)
求め方を変えたい場合はパラメータmethodを追加する。
例:
np.percentile(data, 25, method='weibull')デフォルトのオプションはlinearである。
この9つの方法は R. J. Hyndman and Y. Fan の論文2に沿っているみたい。
linearとweibullの分位数の計算方法は、後ほど見ていく。
statistics.quantile
statistics.quantile は分割方法は2つである。3exclusiveとinclusiveの2つである。デフォルトはexclusiveなので、inclusiveに変更したい場合は、
statistics.quantiles(data, method='inclusive')とする。
また、分割を増やす場合は パラメータ $n$ を設定する。
例
statistics.quantiles(data, n=100, method='inclusive')exclusive は numpy.percentile の weibull,inclusive は numpy.percentile の linear
に該当するようだ。
分位数の計算方法
データ ${X_1, \cdots, X_n}$ に対して、昇順に並べ替えたデータを ${X_{(1)}, \cdots, X_{(n)}}\ (X_{(1)}\leq \cdots\leq X_{(n)})$ とする。
linearの場合
$0<p<1$ とする。linear の $p$ 分位数 $Q_{linear}(p)$ は以下である。
$$
Q_{linear}(p) = (n-1)(X_{(j+1)} – X_{(j)})p + jX_{(j)} + (1-j)X_{(j+1)} \label{1}\tag{1}
$$
ただし、
$$
\frac{j – 1}{n – 1} \leq p < \frac{j}{n – 1} \label{2}\tag{2} $$
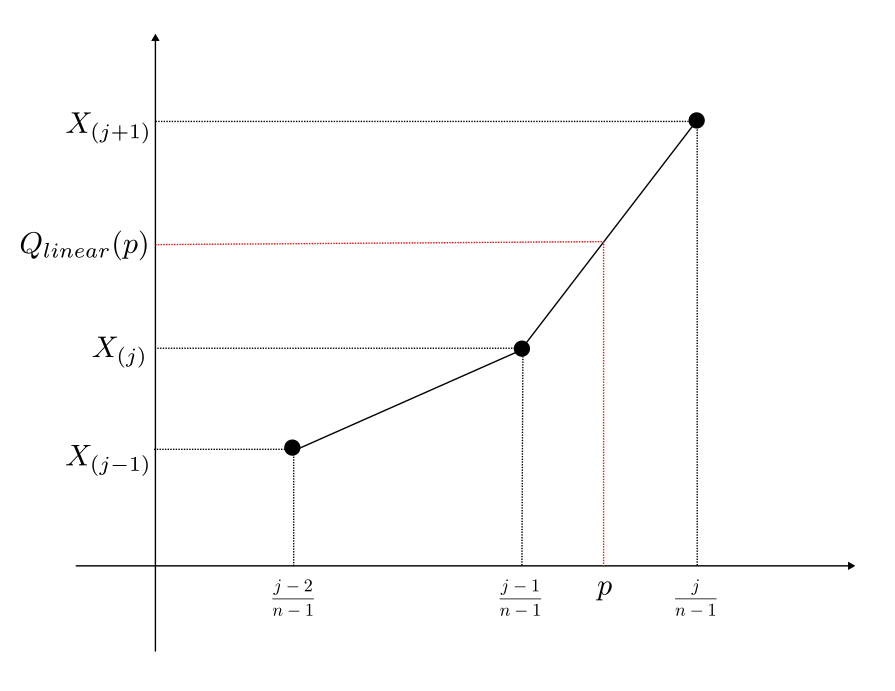
例
イントロダクションで出した例
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
を使って、第一四分位数 $Q_{linear}(1/4)$ を求めてみる。data を昇順に並べ替えると、
[1, 9, 12, 13, 15, 20, 25, 26, 30, 35, 37]
である。まず、$(\ref{2})$ から $j$ を決める。$n = 11,\ p = 1/4$ より、
$$
\frac{j – 1}{10} \leq \frac{1}{4} < \frac{j}{10} \Leftrightarrow \frac{5}{2} < j \leq \frac{7}{2}
$$
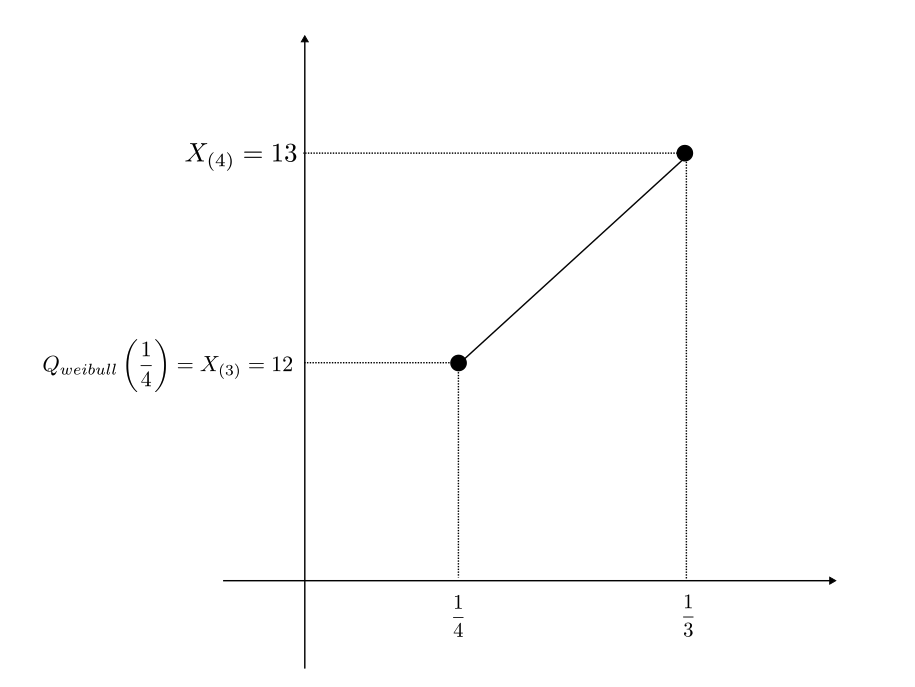
となるので、$j = 3$。よって、$X_{(3)} = 12,\ X_{(4)} = 13$ なので $(\ref{1})$より、
$$
Q_{linear}\left(\frac{1}{4}\right) = 10(X_{(4)} – X_{(3)})\cdot\frac{1}{4} + 3X_{(3)} – 2X_{(4)} = 12.5
$$
となる。
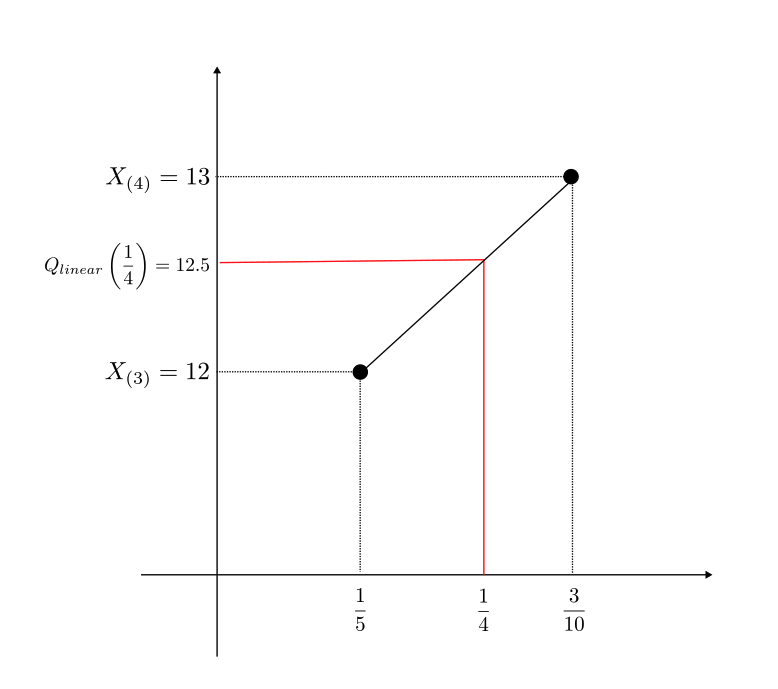
weibullの場合
weibull の $p$ 分位数 $Q_{weibull}(p)$ は以下である。
$$
Q_{weibull}(p) = (n+1)(X_{(j+1)} – X_{(j)})p + (j + 1)X_{(j)} -jX_{(j+1)} \label{3}\tag{3}
$$
ただし、
$$
\frac{j}{n + 1} \leq p < \frac{j + 1}{n + 1} \label{4}\tag{4}
$$
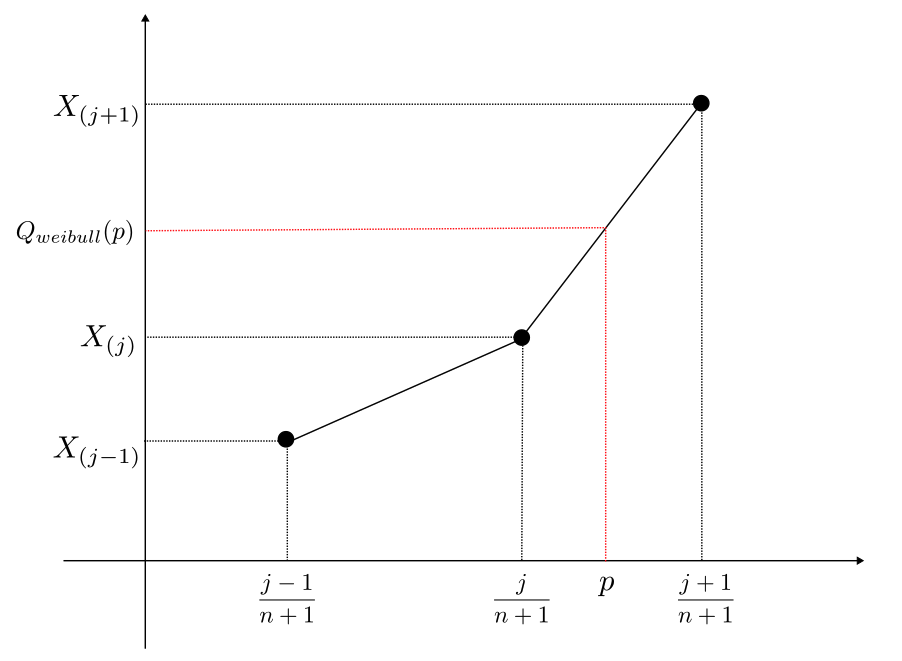
例
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
とし、昇順に整理すると、
[1, 9, 12, 13, 15, 20, 25, 26, 30, 35, 37]
である。$p=1/4$ とすると、$(\ref{4})$ より
$$
\frac{j}{12} \leq \frac{1}{4} < \frac{j+1}{12} \Leftrightarrow 2 < j \leq 3
$$
なので、$j = 3$。
よって $X_{(3)} = 12,\ X_{(4)} = 13$ なので、$(\ref{3})$ より、
$$
Q_{weibull}\left(\frac{1}{4}\right) = 12(X_{(4)} – X_{(3)})\cdot\frac{1}{4} + 4X_{(3)} – 3X_{(4)} = 12
$$
補足
あまり使うことはないだろうが、numpy.percentileのweibull、statistics.quantileのexclusiveでは $p < 1/(n+1)$ のとき $j < 1$ 、そして $p>n/(n+1)$ のとき $j > n$ となる。この場合、numpy.percentileのweibullとstatistics.quantileのexclusiveは結果が異なるようだ。
例えば、
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
としたとき、
import statistics
import numpy as np
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
# 0.01分位数
print(np.percentile(data, 1, method='weibull')) # 結果:1.0
print(statistics.quantiles(data, n=100)[0]) # 結果:-6.04
# 0.99分位数
print(np.percentile(data, 99, method='weibull')) # 結果:37.0
print(statistics.quantiles(data, n=100)[98]) # 結果:38.76となる。
np.percentile に関しては、
$p < 1/(n+1)$ のとき、$Q(p) = X_{(1)}$ $p > n/(n+1)$ のとき、$Q(p) = X_{(n)}$
となることが以下から推測できる。
import matplotlib.pyplot as plt
import numpy as np
# 座標描画用の関数
def plot_cordinate(x, y, color):
plt.plot(x, y, marker='.', color=color)
plt.hlines(y, 0, x, "m", linestyle=":", color=color)
plt.vlines(x, 0, y, "m", linestyle=":", color=color)
plt.annotate(x, xy=(x, 0), xytext=(x, -1.5), ha='center', color=color)
plt.annotate(y, xy=(0, y), xytext=(-1, y), ha='center', color=color)
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
# data を昇順に並べ変える
sorted_data = sorted(data)
# j=1 のときの座標を設定
x1 = 8.3 # p = 1/12
y1 = sorted_data[0] # X_(1)
# j=11 のときの座標を設定
x11 = 91.6 # p = 11/12
y11 = sorted_data[10] # X_(11)
# dataに対してpパーセンタイルを描画
p = np.linspace(0, 100, 6001)
plt.xlim(0,100)
plt.ylim(0,40)
plt.plot(p, np.percentile(data, p, method='weibull'), color='b')
# X_(1)とX_(11)の座標を描画
plot_cordinate(x1, y1, color='r')
plot_cordinate(x11, y11, color='g')
plt.show()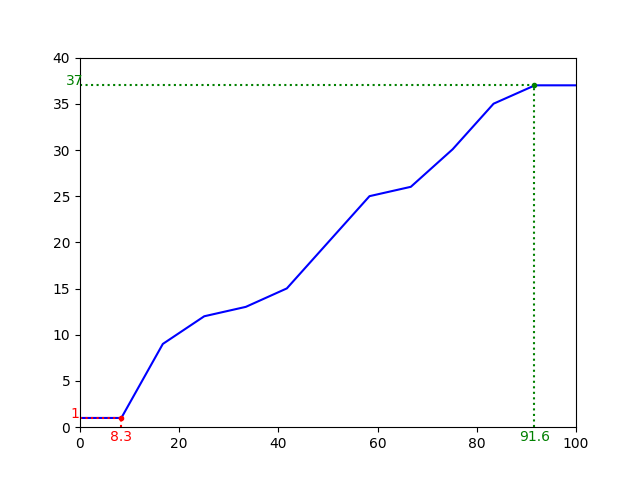
statistics.quantiles は
$p < 1/(n+1)$ のとき、$Q(p)$ は点 $(1/(n+1), X_{(1)})$ と $(2/(n+1), X_{(2)})$ を通る直線上、
$p > n/(n+1)$ のとき、$Q(p)$ は点 $((n-1)/(n+1), X_{(n-1)})$ と $(n/(n+1), X_{(n)})$ を通る直線上、
となることが以下から推測できる
import matplotlib.pyplot as plt
import numpy as np
import statistics
# 座標描画用の関数
def plot_cordinate(x, y, color):
plt.plot(x, y, marker='.', color=color)
plt.hlines(y, 0, x, "m", linestyle=":", color=color)
plt.vlines(x, 0, y, "m", linestyle=":", color=color)
plt.annotate(x, xy=(x, 0), xytext=(x, -1.5), ha='center', color=color)
plt.annotate(y, xy=(0, y), xytext=(-1, y), ha='center', color=color)
# 2点を通る直線の描画の関数
def plot_line(x1, y1, x2, y2, color):
t = np.linspace(0,100,1000)
m = (y1 - y2)/(x1 - x2)
y = (m * (t - x1)) + y1
plt.plot(t, y, linestyle='--', color=color)
data = [26, 12, 30, 20, 35, 25, 1, 37, 15, 13, 9]
# data を昇順に並べ変える
sorted_data = sorted(data)
# j=1 のときの座標を設定
x1 = 8.3 # p = 1/12
y1 = sorted_data[0] # X_(1)
# j=2 のときの座標を設定
x2 = 16.6 # p = 2/12
y2 = sorted_data[1] # X_(2)
# j=10 のときの座標を設定
x10 = 83.3 # p = 10/12
y10 = sorted_data[9] # X_(10)
# j=11 のときの座標を設定
x11 = 91.6 # p = 11/12
y11 = sorted_data[10] # X_(11)
# dataに対してpパーセンタイル(statistics.quantiles)を描画
p = [i for i in range(1, 100)]
plt.xlim(0,100)
plt.ylim(0,40)
plt.plot(p, statistics.quantiles(data, n=100), color='b')
# X_(1), X_(2), X_(10), X_(11)の座標を描画
plot_cordinate(x1, y1, color='r')
plot_cordinate(x2, y2, color='r')
plot_cordinate(x10, y10, color='g')
plot_cordinate(x11, y11, color='g')
# X_(1)とX_(2)を通る直線
plot_line(x1, y1, x2, y2, color='c')
# X_(10)とX_(11)を通る直線
plot_line(x10, y10, x11, y11, color='m')
plt.show()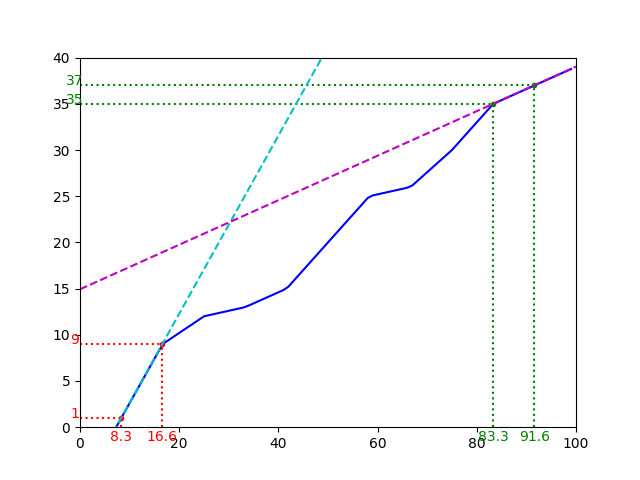
実際、$p=1/100$ で計算をしてみると、
$$
\frac{j}{12} \leq p < \frac{j+1}{12}
$$
を満たす $j$ は
$$
-\frac{88}{100} < j \leq \frac{12}{100}
$$
となるため、$j<1$である。$(1/12, X_{(1)})$ と $(2/12, X_{(2)})$ を通る直線の式は
$$
Q(p) = 96p-7
$$
である。よって、$Q(1/100) = -6.04$ となることが確認できた。
参考
- numpy.percentile — NumPy v2.0 Manual ↩︎
- R. J. Hyndman and Y. Fan, “Sample quantiles in statistical packages,” The American Statistician, 50(4), pp. 361-365, 1996 ↩︎
- statistics — 数学的統計関数 — Python 3.12.4 ドキュメント ↩︎