※ この記事はnoteをやっていた頃に投稿した記事です。こちらのブログに移しました。
(note投稿日:2022年10月23日)
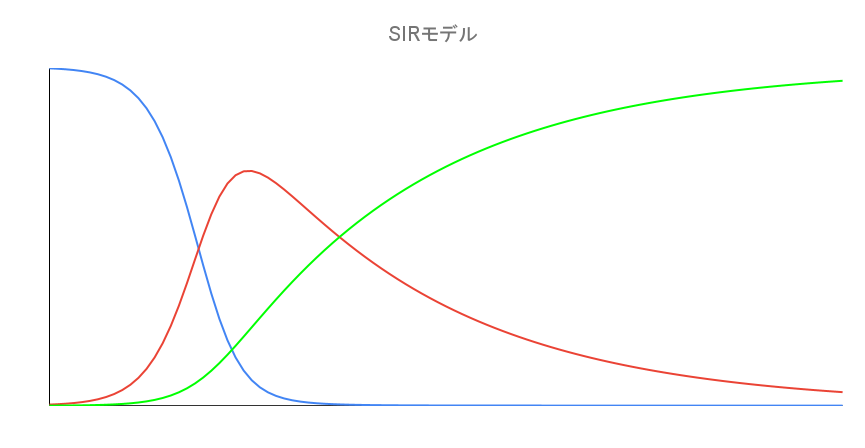
SIRモデルとは
- 1972年にWilliam Ogilvy Kermack と Anderson Gray McKendrick により発表された感染症モデル
- SIRとは以下の頭文字で、それらにより式が構成される
- S : 感受性者(Susceptible)
- I : 感染者(Infected)
- R : 回復した人、死亡した人(recovered, removed)
- つまり、Sはこれから感染する可能性がある人達、Iは感染した人達、Rは感染後回復した人達もしくは死亡者である
式
時刻$t$に対して、
$S(t)$ : 感受性者数
$I(t)$ : 感染者数
$R(t)$ : 回復した人や死亡者の数
とする。
このとき、SIRモデルは以下のように表される。
$$
\begin{split}
\frac{dS(t)}{dt} &= -\beta S(t)I(t) \
\frac{dI(t)}{dt} &= \beta S(t)I(t) – \gamma I(t) \
\frac{dR(t)}{dt} &= \gamma I(t)
\end{split}
$$
ただし、$\beta$は感染率、$\gamma$は回復率を表す。
イメージ
次のような例で考えてみる。
- 全体人数は12人(12人同じ空間にいるとする)
- このうち1人があるウイルスに感染してしまったとする
- すなわち、感受性者数は11人、感染者数1人
- このウイルスは感染者と接触すると1日あたり0.1の確率で感染するとする
- 感染した人は2日で回復するとする
1日目
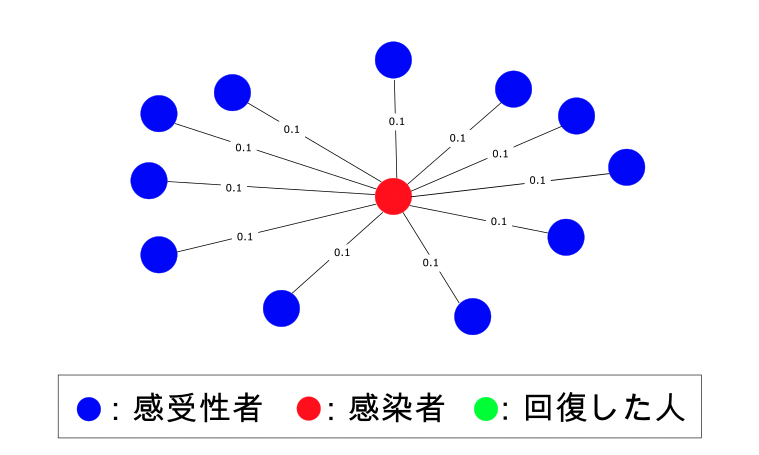
- 感受性者:11人
- 感染者:1人
- 回復した人:0人
1日目→2日目
感受性者は11人、感染者は1人より感受性者と感染者との接触回数は11回となる。
また、1日あたり感受性者が感染者と接触すると0.1の確率で感染するので、
$$11\times 0.1 = 1.1$$
より感受性者から1人(小数点以下切り捨て)感染してしまう。
回復には2日かかるので、1日目の段階では回復した人は0人である。
なので、
- 感受性者:11人→10人
- 感染者:1人→2人
- 回復した人:0人→0人
となる。
2日目
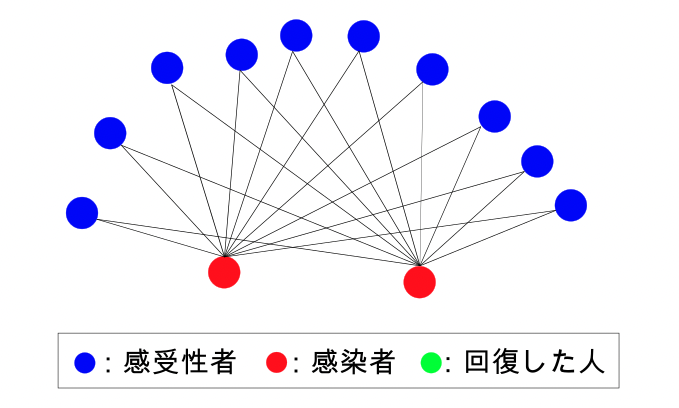
- 感受性者:10人
- 感染者:2人
- 回復した人:0人
2日目→3日目
1日目→2日目の場合と同様に考えると、
感受性者は10人、感染者は2人より感受性者と感染者との接触回数は$10\times 2 = 20$回となる。
また、1日あたり感受性者が感染者と接触すると0.1の確率で感染するので、
$$20\times 0.1 = 2$$
より感受性者から2人感染してしまう。
回復に関しては1日目感染してた1人が回復する。
- 感受性者:10人→8人
- 感染者:2人→3人
- 回復した人:0人→1人
3日目
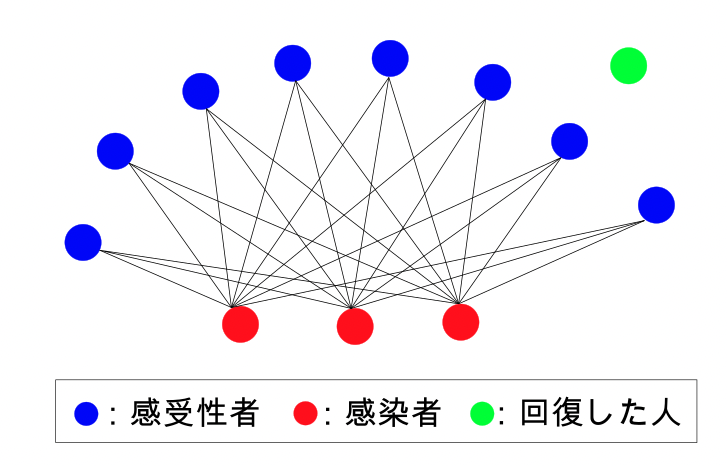
- 感受性者:8人
- 感染者:3人
- 回復した人:1人
3日目→4日目
感受性者は8人、感染者は3人より感受性者と感染者との接触回数は$8\times 3 = 24$回となる。
また、1日あたり感受性者が感染者と接触すると0.1の確率で感染するので、
$$24\times 0.1 = 2.4$$
より感受性者から2人(小数点以下切り捨て)感染してしまう。
回復する人は、2日目に感染した2名が回復する。
よって、
- 感受性者:8人→6人
- 感染者:3人→3人
- 回復した人:1人→3人
というような感じになる。
まとめ
感受性者と感染者の接触回数は
$$\text{感受性者}\times \text{感染者}$$
となるので、感受性者が感染者になる人数は、
$$\text{感受性者}\times \text{感染者}\times 感染率$$
また、感染者が回復する人数は、
$$\text{感染者}\times 回復率$$
となる。
※上の例では切り捨てで考えているため少しイメージしにくいが、今回の例では2日で回復するとしているので回復率は0.5としている。
数列モデル
上の例を参考に数列モデルを立てていく
$N$ : 全体の人数
$S_n$ : $n$日目の感受性者数
$I_n$ : $n$日目の感染者数
$R_n$ : $n$日目の回復した人の数
$\beta$ : 感染率
$\gamma$ : 回復率 ($1/\gamma$日で回復)
とする。
このとき、
$$S_n + I_n + R_n = N$$
- 感受性者に関して
$n$日目から$n+1$日目にかけての感受性者数は
$$\beta S_n I_n \text{ (人)}$$
減る。
つまり、
$$S_{n+1} – S_n = -\beta S_n I_n$$
- 回復に関して
$n$日目から$n+1$日目にかけての回復した人数は
$$\gamma I_n \text{ (人)}$$
増える。
よって、
$$R_{n+1} – R_n = \gamma I_n$$
- 感染者に関して
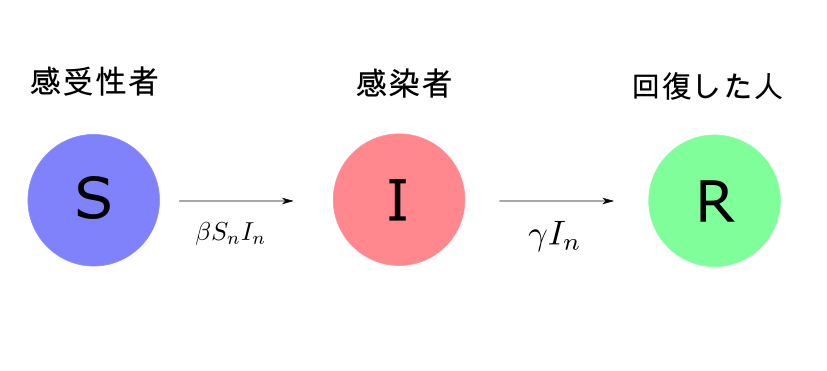
$n$日目から$n+1$日目にかけて、
感受性者から感染者へ$\beta S_n I_n$人移り、
感染者から回復した人は$\gamma I_n$人移る。
よって、$n$日目から$n+1$日目にかけての感染者は
$$\beta S_n I_n – \gamma I_n \text{ (人)}$$
増える。
※「感受性者」から「感染者」への人数が「感染者」から「回復した人」への人数よりも少なかった場合、感染者の人数は減っていく。
すなわち、$n$日目から$n+1$日目にかけての感染者は
$$\gamma I_n – \beta S_n I_n \text{ (人)}$$
減る。
よって、
$$I_{n+1} – I_n = \beta S_n I_n – \gamma I_n$$
以上のことから、
$$
\begin{cases}
S_{n+1} – S_n = -\beta S_n I_n \\
I_{n+1} – I_n = \beta S_n I_n – \gamma I_n \\
R_{n+1} – R_n = \gamma I_n
\end{cases}
$$
となる。