※ この記事はnoteをやっていた頃に投稿した記事です。こちらのブログに移しました。
(note投稿日:2022年11月6日)
関連記事
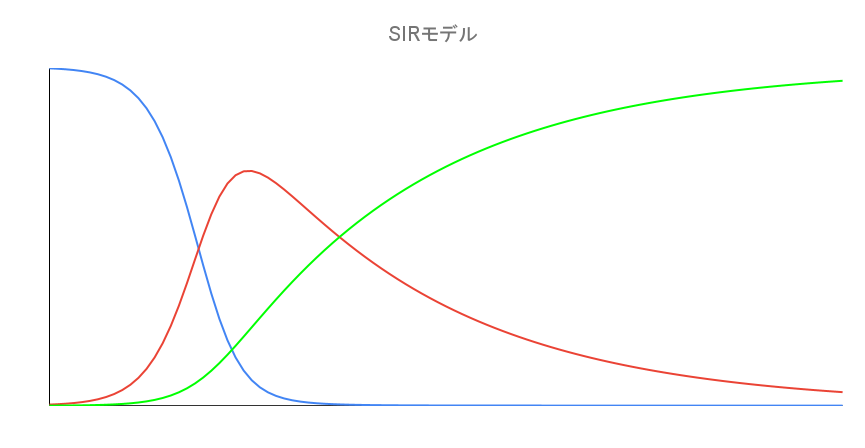
SIR数列モデル
記号
$N$ : 人口
$S_n$ : $n$日目の感受性者数
$I_n$ : $n$日目の感染者数
$R_n$ : $n$日目の回復した人数
$\beta$ : 感染率
$\gamma$ : 回復率
式
$$
\begin{cases}
S_{n+1} – S_n = -\beta S_n I_n \\
I_{n+1} – I_n = \beta S_n I_n – \gamma I_n \\
R_{n+1} – R_n = \gamma I_n
\end{cases}
$$
設定
次のような状況を考える。
$N = 10000000$ (人口一千万人)
$I_1 = 1$ (感染者数1人)
$S_1 = 9999999$
$R_1 = 0$
$\gamma = 0.1$ (感染したら10日で回復)
感染率について
前回は全体を12人とし、その12人全員が毎日接触するとしていた。今回は以下のように設定する。
- 感染者1人に対し、1日10人と接触する
- 感染者と感受性者が接触すると1日あたり0.05の確率で感受性者が感染するとする
$n$日目、感受性者の割合は$S_n/N$である。
なので、感染者1人が誰か1人(感受性者または感染者または回復した人)と接触する場合、感染する可能性のある人の割合は$S_n/N$となる。
$n$日目の感染者数が$I_n$で、感染者1人に対し、1日10人と接触するとしているので、接触したとき感染する確率(0.05)を無視すると、感染者数は
$$10 \times I_n \times S_n/N$$
となる。
よって、接触したとき感染する確率0.05を含ると、$n$日目から$n+1$日目にかけての感染者数は
$$0.05 \times 10 \times I_n \times S_n/N$$
以上のことから感染率$\beta$は
$$\beta = 0.05 \times 10 / N$$
とすることにする。
googleのスプレッドシートでグラフ化してみる
項目を作成する
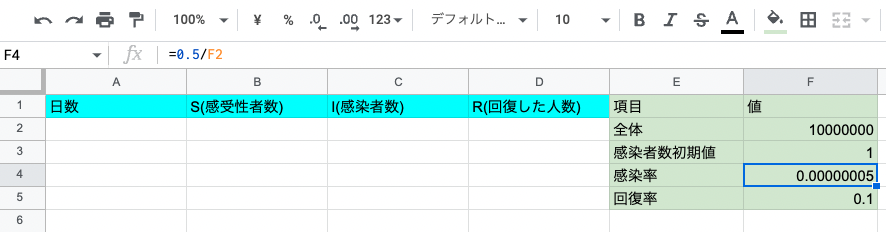
- 一行目に「日数」「感受性者数」「感染者数」「回復した人数」の項目を作成する。
- 上とは別の列に初期値に必要な項目とその値を設定する
- 感染率は0.5/Nとしている
初期値の設定
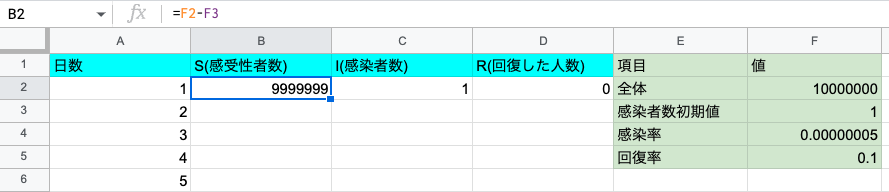
- 日数を記入
- 今回は100日ぐらいまで調べようと思うので1から100までA列に記入
- 回復した人数は「0」
- 感染者数は「感染者数初期値」
- 図のスプレッドシートでは「=F3」
- 感受性者数は「全体-感染者数初期値」
- 図のスプレッドシートでは「=F2-F3」
2日目の感受性者数
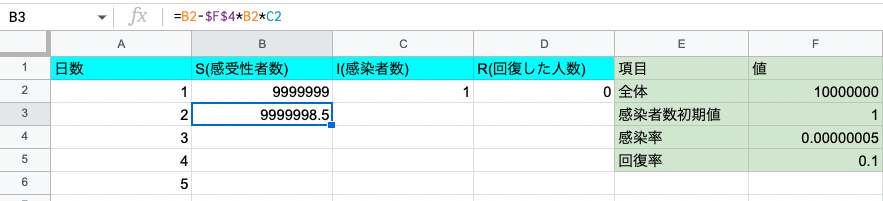
- $S_2 = S_1 – \beta S_1 I_1$より、感受性者数の列の2日目のセルに式「$S_1 – \beta S_1 I_1$」を記入する
- 図のスプレッドシートでは「=B2-\$F$4*B2*C2」
- 感染率$\beta$は固定のため、シートのF4は$マークをつけておく
2日目の感染者数
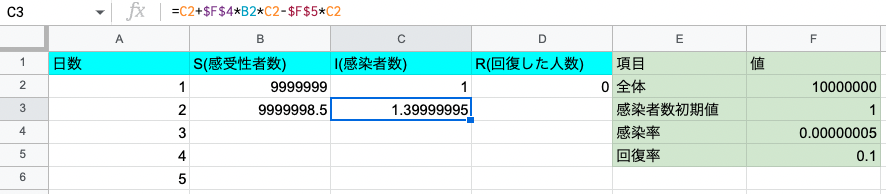
- $I_2 – I_1 = \beta S_1 I_1 – \gamma I_1$より、感染者数の列の2日目のセルに式「$I_1 + \beta S_1 I_1 – \gamma I_1$」を記入する
- 図のスプレッドシートでは「=C2+\$F\$4*B2*C2-\$F$5*C2」
- 感染率$\beta$と回復率$\gamma$は固定のため、シートのF4とF5は$マークをつけておく
2日目の回復した人数
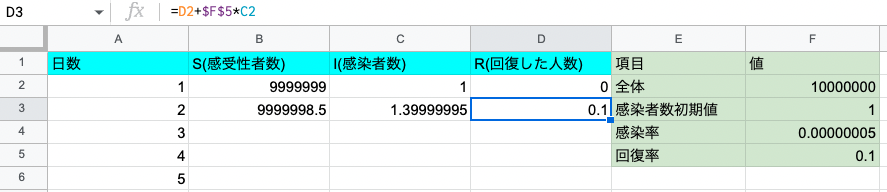
- $R_2 – R_1 = \gamma I_1$より、回復した人数の列の2日目のセルに式「$R_1 + \gamma I_1$」を記入する
- 図のスプレッドシートでは「=D2+\$F$5*C2」
- 回復率$\gamma$は固定のため、シートのF5は$マークをつけておく
n日目の感受性者数、感染者数、回復した人数
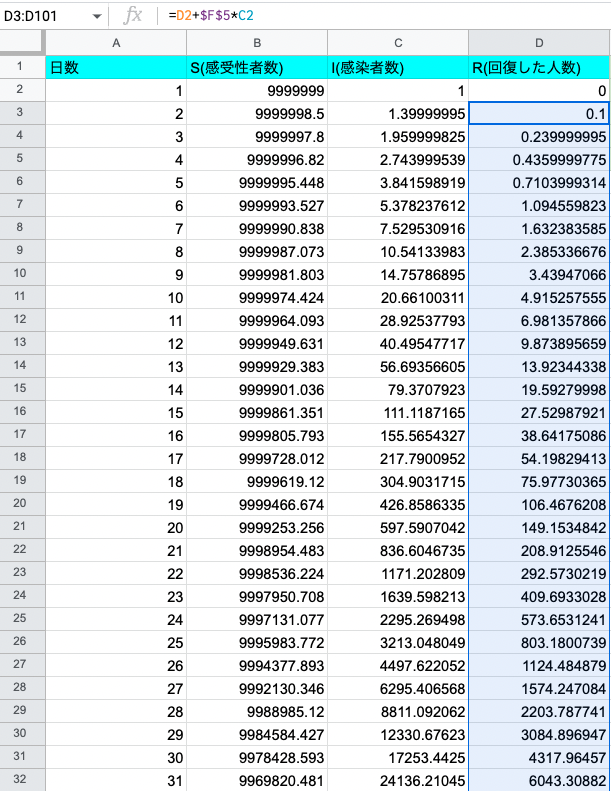
- 感受性者数、感染者数、回復した人数それぞれの列で2日目の行のセルの右下にカーソルを合わせて100日目までクリックしながら下にスライドさせる
グラフ挿入
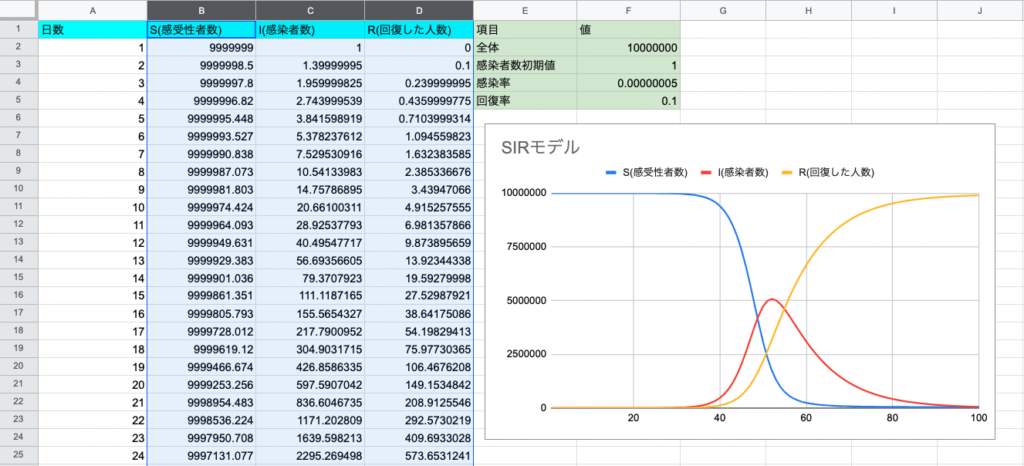
- 感受性者数と感染者数と回復した人数の列を選択し、挿入→グラフをクリック
- すると折れ線グラフがいい感じに現れる
- 後はタイトル変えたり、横軸に日数を付け加えたりなどグラフの微調整をする