※ この記事はnoteをやっていた頃に投稿した記事です。こちらのブログに移しました。
(note投稿日:2022年11月17日)
関連記事
前回までのおさらい
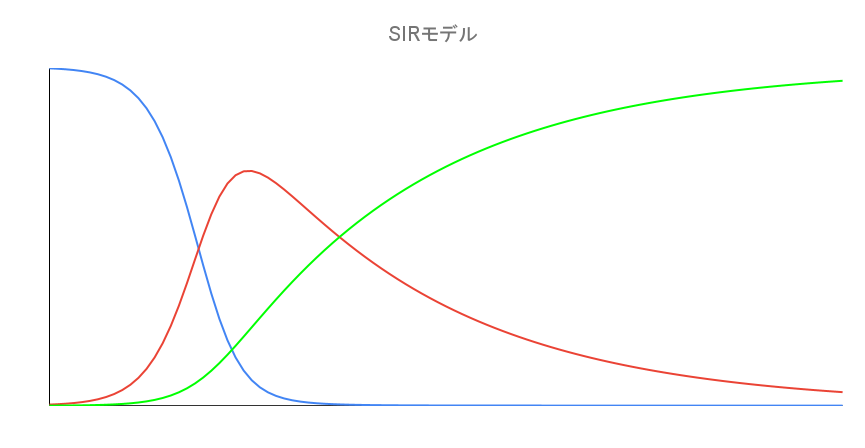
SIR数列モデル
$N$ : 人口
$S_n$ : $n$日目の感受性者数
$I_n$ : $n$日目の感染者数
$R_n$ : $n$日目の回復した人数
$\beta$ : 感染率
$\gamma$ : 回復率
としたとき、SIR数列モデルは
$$
\begin{cases}
S_{n+1} – S_n = -\beta S_n I_n \\
I_{n+1} – I_n = \beta S_n I_n – \gamma I_n \\
R_{n+1} – R_n = \gamma I_n
\end{cases}
$$
と表される。
初期値
以下の値をベースに考えていく。
$N = 10000000$
$I_1 = 1$
$S_1 = 9999999$
$R_1 = 0$
$\beta = 0.5/N = 0.00000005 $
$\gamma = 0.1$ (感染したら10日で回復)
感染者数の増減について
感染者数に着目してみる。
$$I_{n+1} – I_n = \beta S_n I_n – \gamma I_n$$
これは、$n$日目から$n+1$日目にかけての感染者数の増減を表している。
$n$日目から$n+1$日目にかけての感染者数は
$$I_{n+1} – I_n > 0$$
のとき、増えていき、
$$I_{n+1} – I_n < 0$$
のとき、減っていく。
すなわち、
$$
\begin{split}
\beta S_n I_n – \gamma I_n &> 0 \
S_n &> \frac{\gamma}{\beta}
\end{split}
$$
を満たすとき、$n+1$日目にかけて感染者数が増加する。
逆に、
$$S_n < \frac{\gamma}{\beta}$$
を満たすとき、感染者数は減少する。
今回は、$\beta = 0.00000005$, $\gamma = 0.1$より
$$\frac{\gamma}{\beta} = 2000000$$
実際前回作ったデータを確認すると、
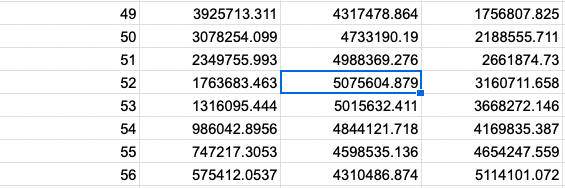
感受性者数の51日目までは2000000を超えていて、52日目以降は2000000を下回っている。
一方で、感染者数は52日目が最大である。
基本再生産数
基本再生産数(basic reproduction number) $\mathscr{R}_0$を
$$\mathscr{R}_0 = \frac{\beta N}{\gamma}$$
と表す。基本再生産数とは簡単に言うと、1人の感染者が感受性者を感染させる人数の期待値である。
例えば、基本再生産数$\mathscr{R}_0 = 2$の場合、
1→2→4→8→…
と感染者が増えていく。
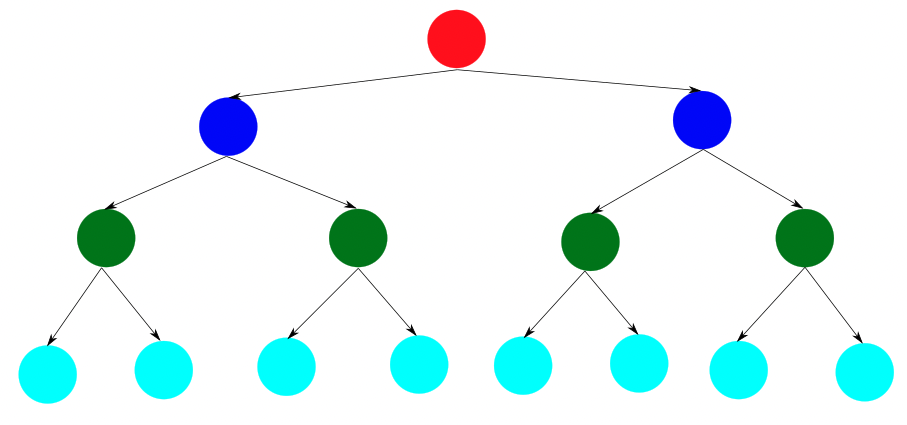
今使っているデータだと分かりづらいので、少し強引ではあるが、$\beta = 2/N$, $\gamma = 1$とする。(感染すると1日で回復するとし1日の感染者数の増加を見てみる。)

感染者数がほぼ1→2→4→8となっていることが図から読み取れる。一般的には、$S_n\approx N$とすることにより1人の感染者が感受性者に影響を及ぼす数が$\mathscr{R}_0$であることが分かる。
※基本再生産数は感受性者数を全体の人数$N$として考えている。しかし、上の感染者数の増減でやったみたいに、感受性者数や感染者数によって感染者数の増え方が変わったり、減少もする。つまり、時間や日によって感受性者が減ったり、回復する人の人数が増えるので、1人の感染者が感受性者を感染させる人数は変化する。このような再生産数を 実効再生産数(effective reproduction number) と呼び、
$$\mathscr{R}_e(n) = \frac{\beta S_n}{\gamma}$$
と表す。
イメージとしては、誰も感染していない集団の中に1人感染者を入れたとき、その感染者が感染させる人数が基本再生産数。日によって変わっていく感受性者数、感染者数、回復した人数全て考慮したときに、ある日感染した感染者1人が感受性者を感染させる人数が実効再生産数である。
実効再生産数と感染者数の増減の関係
感染者は
$$\beta S_n I_n – \gamma I_n > 0$$
のとき増加し、
$$\beta S_n I_n – \gamma I_n < 0$$
のとき減少する。
$$\beta S_n I_n – \gamma I_n = \gamma I_n \left( \frac{\beta}{\gamma} S_n – 1 \right)$$
で、$\gamma I_n > 0$より、
$$
\begin{split}
\frac{\beta}{\gamma} S_n – 1 &> 0 \
\frac{\beta}{\gamma} S_n &> 1 \
\mathscr{R}_e(n) &> 1
\end{split}
$$
のとき、感染者数は増加し、逆に
$$\mathscr{R}_e(n) < 1$$
のとき感染者数は減少する。
感染者数の最大値について
結論から述べると、基本再生産数が1より大きいとき、一日の感染する人数の最大値を減らすためには基本再生産数を小さくすれば良い。
例を見てみる。
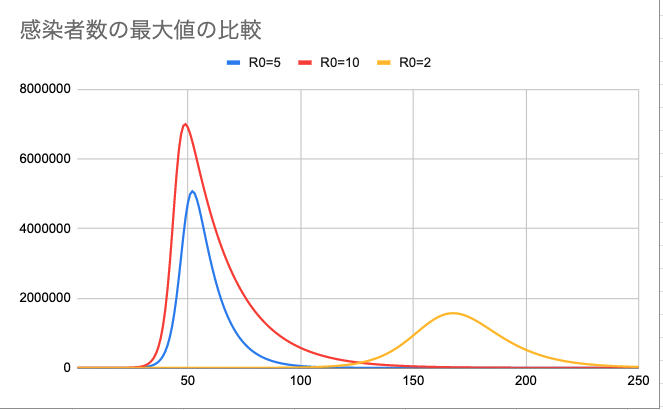
- 青色のグラフは前回考えたデータ同様$\beta = 0.5/N,\ \gamma = 0.1$。すなわち、$\mathscr{R}_0 = 5$。
- 赤色のグラフは回復率を下げて$\beta = 0.5/N,\ \gamma = 0.05$。すなわち、$\mathscr{R}_0 = 10$。
- 黄色のグラフは感染率を下げて$\beta = 0.2/N,\ \gamma = 0.1$。すなわち、$\mathscr{R}_0 = 2$。
基本再生産数を上げると感染者数の最大値が上がり、基本再生産数を下げると感染者数の最大値が下がっていることがグラフから見て取れる。
微分方程式のSIRモデルから感染者数の最大値を調べる
時刻$t$に対して、
$S(t)$ : 感受性者数
$I(t)$ : 感染者数
$R(t)$ : 回復した人や死亡者の数
としたとき、SIRモデルは、
$$
\begin{split}
\frac{dS(t)}{dt} &= -\beta S(t)I(t) \\
\frac{dI(t)}{dt} &= \beta S(t)I(t) – \gamma I(t) \\
\frac{dR(t)}{dt} &= \gamma I(t)
\end{split}
$$
である。
時刻$t=0$における回復した人数を
$$R(0) = 0$$
基本再生産数$\mathscr{R}_0$を
$$\mathscr{R}_0 = \frac{\beta}{\gamma}$$
実効再生産数$\mathscr{R}_e(t)$を
$$\mathscr{R}_e(t) = \frac{\beta}{\gamma}S(t)$$
とする。また、
$$\mathscr{R}_e(0)>1$$
とする、すなわち時刻$t=0$の時点では感染者は増加する。
$$\frac{dS}{dI} = -\frac{\beta SI}{\beta SI – \gamma I}$$
より、
$$
\int\frac{\beta S – \gamma}{\beta S}dS = -\int dI
$$
となり、これを解くと、
$$I + S – \frac{\gamma}{\beta}\log S = C $$
となる。ただし、$C$は定数。$C$は定数なので、
$$
\begin{split}
C &= I(0) + S(0) – \frac{\gamma}{\beta}\log S(0) \
&= N – \frac{\gamma}{\beta}S(0)
\end{split}
$$
と書ける。
$\frac{dI}{dt} = 0$を満たすとき、$I$は最大値を持つ。このとき、$
S = \frac{\gamma}{\beta}$となるので、$I$の最大値を$I_{max}$とすると、
$$
\begin{split}
I_{max} &= \frac{\gamma}{\beta}\cdot \log \frac{\gamma}{\beta} – \frac{\gamma}{\beta} + C \\
&= \frac{\gamma}{\beta}\cdot \log \frac{\gamma}{\beta} – \frac{\gamma}{\beta} + N – \frac{\gamma}{\beta}\log S(0) \\
&= \frac{\gamma}{\beta}\left(\log \frac{\gamma}{\beta} – 1 – \log S(0)\right) + N \\\
&= \frac{N}{\mathscr{R}_0}\left(\log \frac{N}{\mathscr{R}_0} – 1 – \log S(0)\right) + N
\end{split}
$$
となる。
よって、
$$
\frac{dI_{max}}{d\mathscr{R}_0} = \frac{N\left(\log\mathscr{R}_0 – \log \frac{N}{S(0)}\right)}{\mathscr{R}_0^2}
$$
より、$I_{max}$の増減表は
$$
\begin{array}{|c|c|c|c|c|}
\hline
\mathscr{R}_0 & 0 & \cdots & N/S(0) &\cdots \\
\hline
I_{max}’ & \diagup & – & 0 & + \\
\hline
I_{max} & \diagup & \searrow & N – S(0) & \nearrow \\
\hline
\end{array}
$$
となるので、
$$\mathscr{R}_0 > \frac{N}{S(0)}$$
すなわち、
$$\mathscr{R}_e(0) > 1$$
のとき$\mathscr{R}_0$が増加すると感染者数の最大値も増える。
以上のことから、$t = 0$における実効再生産数が1よりも大きいとき、基本再生産数が小さければ小さいほど(すなわち、感染率が小さいもしくは回復率が大きいほど)感染者数は抑えられる。
ただし、初期の段階では感受性者数が十分大きいため、$S(0)\approx N$としたとき、基本再生産数が1よりも大きいとき、基本再生産数が小さければ小さいほど感染者数は抑えられる。
さまざまな感染症モデル
SIRモデルは感染症モデルの中でも一番基本的なモデルでよく知られている。しかし、SIRモデルは一度回復すると二度と感染することがないモデルとなっているので周期的な流行には向かないモデルである。
感染症モデルはSIRモデル以外にも様々なモデルが発表されている。
例えば、
- 感受性と感染を行き来するSISモデル
- 感染症が潜伏期間も考慮したSEIRモデル
などがある。
まとめ
- 誰も感染していない集団の中に1人感染者を入れたとき、その感染者が感染させる数を基本再生産数と呼び
$$(\text{感染率}/\text{回復率})\times 全体の人数$$
と表される。
- $n$日目、1人の感染者が感受性者に影響を及ぼす数を実効再生産数と呼び
$$(\text{感染率}/\text{回復率})\times n\text{日目の感受性者数}$$
と表される。
- 実効再生産数が1より大きい日は次の日感染者数は増加し、1よりも小さい日は次の日感染者数は減少する。
- 初期の段階では感受性者が十分大きいため、感受性者数と全体の人数が近似しているとすると、基本再生産数が1よりも大きいときは感染拡大し、1よりも小さい時は感染の拡大がないと見込まれる。
- 初日における実行再生産数が1よりも大きいとき(初日の段階で感染拡大が見込まれるとき)、基本再生産数が小さければ小さいほど感染者数を抑えることができる。すなわち、感染者数を極力抑えるためには、感染率を落としたり回復率を上げたりすることである。
- 初期の段階では感受性者が十分大きいため、感受性者数と全体の人数が近似しているとすると、基本再生産数が1よりも大きいとき、基本再生産数が小さければ小さいほど感染者数を抑えることができる。
- 感染症モデルはSIRモデル以外にも色々ある。