関連記事
空間ベクトルの1次独立
このページでは特に断りがない限り、2つ以上のベクトルを考える際、始点は同じ位置にあるものとする。
定義
以下を満たすとき、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立であるという。
$$
k\vec{a} + l\vec{b} + m\vec{c} = \vec{0} \Rightarrow k = l = m = 0
$$
例1
$$
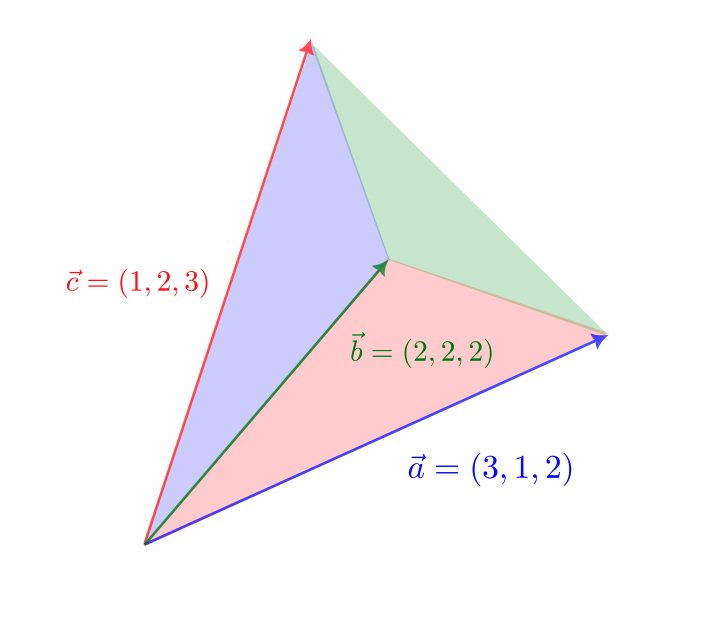
\vec{a} = (3,1,2),\ \vec{b} = (2,2,2),\ \vec{c} = (1,2,3)
$$
とする。

$$
k\vec{a} + l\vec{b} + m\vec{c} = (3k + 2l + m, k + 2l + 2m, 2k + 2l + 3m)
$$
より、$k\vec{a} + l\vec{b} + m\vec{c} = \vec{0}$ とすると、
$$
\begin{cases}
3k + 2l + m = 0 \\
k + 2l + 2m = 0 \\
2k + 2l + 3m = 0
\end{cases}
$$
となる。この連立方程式を解くと、$k = l = m = 0$ となるので、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立である。
例2
$$
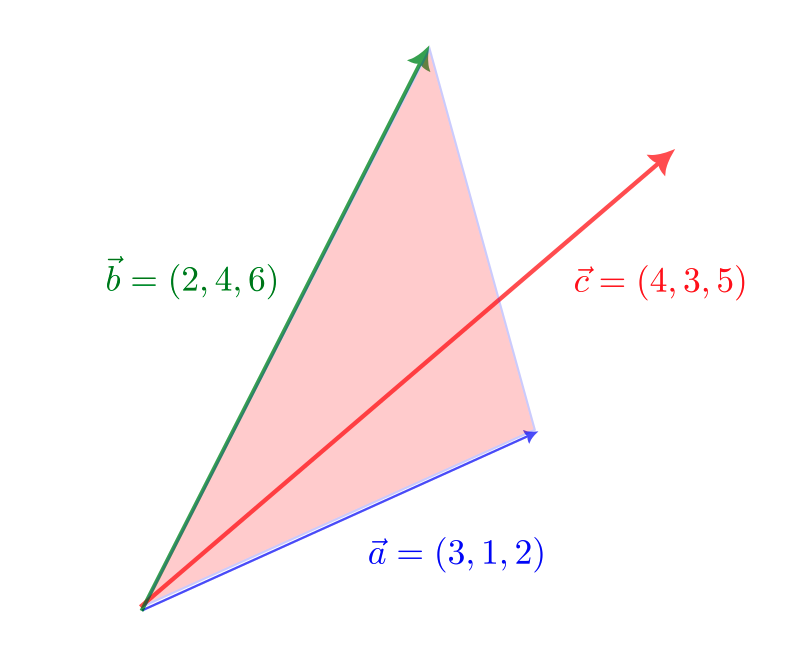
\vec{a} = (3,1,2),\ \vec{b} = (2,4,6),\ \vec{c} = (4,3,5)
$$
とする。

$$
k\vec{a} + l\vec{b} + m\vec{c} = (3k + 2l + 4m, k + 4l + 3m, 2k + 6l + 5m)
$$
より、$k\vec{a} + l\vec{b} + m\vec{c} = \vec{0}$ とすると、
$$
\begin{cases}
3k + 2l + 4m = 0 \\
k + 4l + 3m = 0 \\
2k + 6l + 5m = 0
\end{cases}
$$
となる。例えば、$k=2, l=1,m=-2$ はこの連立方程式の解になり、$k=l=m=0$ 以外の解を持つため、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は1次独立ではない。
また、
$$
\vec{c} = \vec{a} + \frac{1}{2}\vec{b}
$$
と表すことができ、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にある。
空間ベクトルにおける1次独立の性質
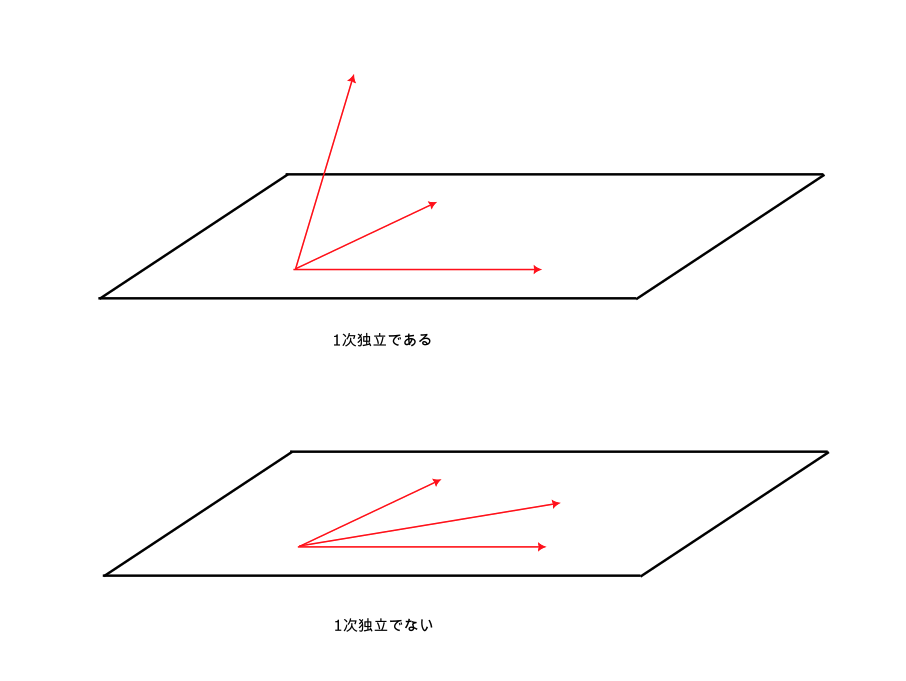
$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立である $\Leftrightarrow$ $\vec{a}\neq\vec{0},\vec{b}\neq\vec{0},\vec{c}\neq\vec{0}$ であり、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にない
証明
まず、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立である $\Rightarrow$ $\vec{a}\neq\vec{0},\vec{b}\neq\vec{0},\vec{c}\neq\vec{0}$ であり、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にないことを示す。
$\vec{a}=\vec{0}$ とする。
このとき、$k=1,l=m=0$ としても $k\vec{a}+l\vec{b}+m\vec{c}=\vec{0}$ が成り立つので、$\vec{a}\neq \vec{0}$ である。
$\vec{b}\neq\vec{0},\vec{c}\neq\vec{0}$ も同様。
$\vec{a}\neq\vec{0},\vec{b}\neq\vec{0},\vec{c}\neq\vec{0}$ で $\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上であるとする。
このとき、
$$
\vec{c} = s\vec{a} + t\vec{b}
$$
と表すことができるので、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は一次独立でない。
よって、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にない。
次に $\vec{a}\neq\vec{0},\vec{b}\neq\vec{0},\vec{c}\neq\vec{0}$ であり、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にない $\Rightarrow$ $\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立であることを示す。
$k\vec{a}+l\vec{b}+m\vec{c}=\vec{0}$ とする。
$k,l,m$ の少なくとも1つは 0 でないとする。
例えば、$m\neq0$ とすると、
$$
\vec{c} = -\frac{k}{m}\vec{a} – \frac{l}{m}\vec{b}
$$
と表すことが出来るため、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ は同一平面上にあるため矛盾する。
よって、$\vec{a}$ と $\vec{b}$ と $\vec{c}$ が1次独立である。


