事前知識
$y = \sin x$
簡単に点を取ってみる
簡単に求められる範囲で、 $y=\sin x\ (0\leq x\leq 2\pi)$ の表は以下となる。
| $x$ | 0 | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ |
|---|---|---|---|---|---|
| $y$ | 0 | $\frac{1}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{\sqrt{3}}{2}$ | 1 |
| $x$ | $\frac{2}{3}\pi$ | $\frac{3}{4}\pi$ | $\frac{5}{6}\pi$ | $\pi$ |
|---|---|---|---|---|
| $y$ | $\frac{\sqrt{3}}{2}$ | $\frac{1}{\sqrt{2}}$ | $\frac{1}{2}$ | 0 |
| $x$ | $\frac{7}{6}\pi$ | $\frac{5}{4}\pi$ | $\frac{4}{3}\pi$ | $\frac{3}{2}\pi$ |
|---|---|---|---|---|
| $y$ | $-\frac{1}{\sqrt{2}}$ | $-\frac{1}{\sqrt{2}}$ | $-\frac{\sqrt{3}}{2}$ | $-1$ |
| $x$ | $\frac{5}{3}\pi$ | $\frac{7}{4}\pi$ | $\frac{11}{6}\pi$ | $2\pi$ |
|---|---|---|---|---|
| $y$ | $-\frac{\sqrt{3}}{2}$ | $-\frac{1}{\sqrt{2}}$ | $-\frac{1}{2}$ | 0 |
上記の表の通りに点を取ってみると以下のような図になる。
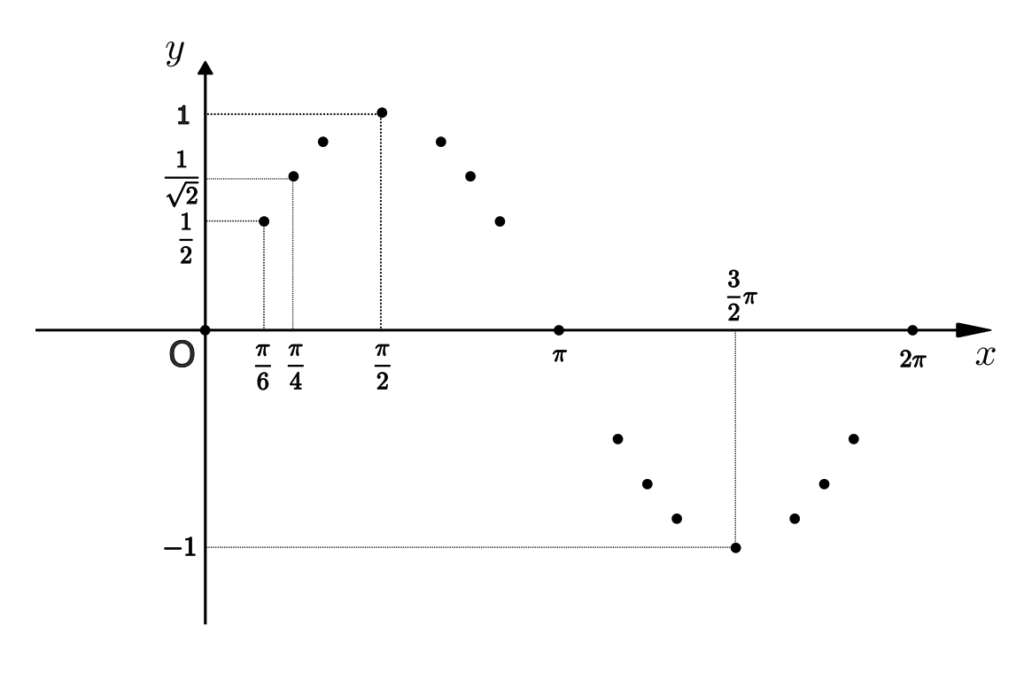
なんとなく、$0 < x < \frac{\pi}{2}$ では増加、$\frac{\pi}{2} < x < \frac{3}{2}\pi$ では減少、$\frac{3}{2}\pi < x < 2\pi$ では増加していることが分かる。
もう少し詳しく見てみる
単位円(半径1の円)を考える。
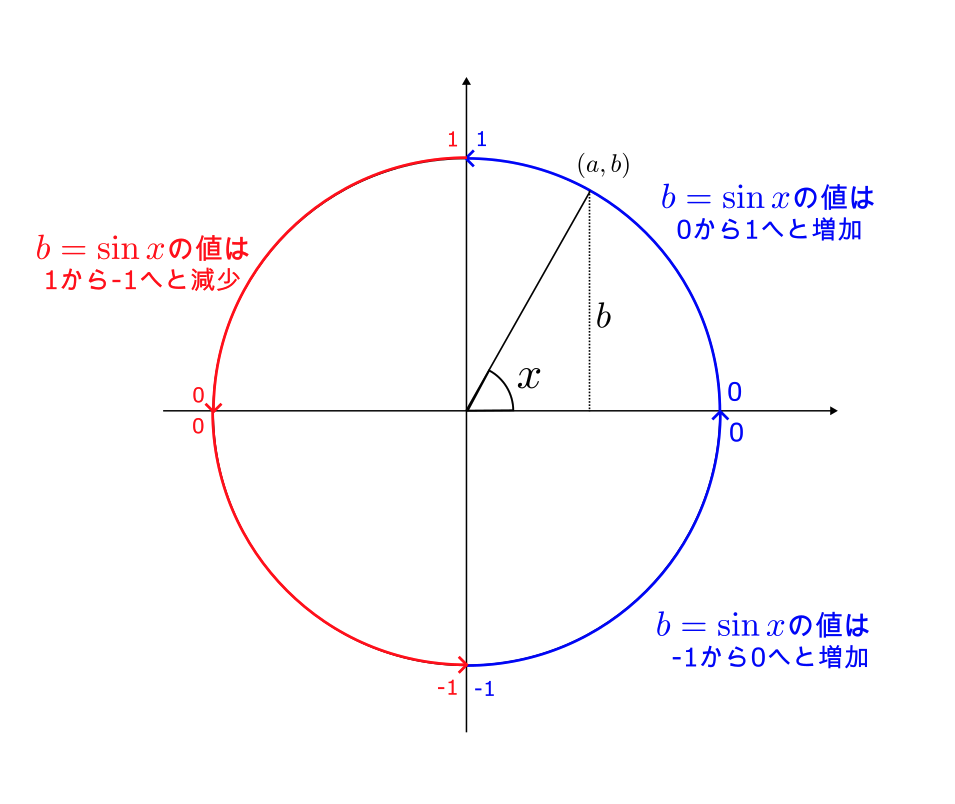
図のように、角度 $x$ に対する円周上の点を $(a,b)$ としたとき、$\sin x = b$ となる。
角度 $x$ が増加すると、$b$ の値は $0 < x < \frac{\pi}{2}$ では 0 から 1 に向かって増加し、$\frac{\pi}{2} < x < \frac{3}{2}\pi$ では 1 から $-1$ に向かって減少し、$\frac{3}{2}\pi < x < 2\pi$ では $-1$ から 0 に向かって増加する。
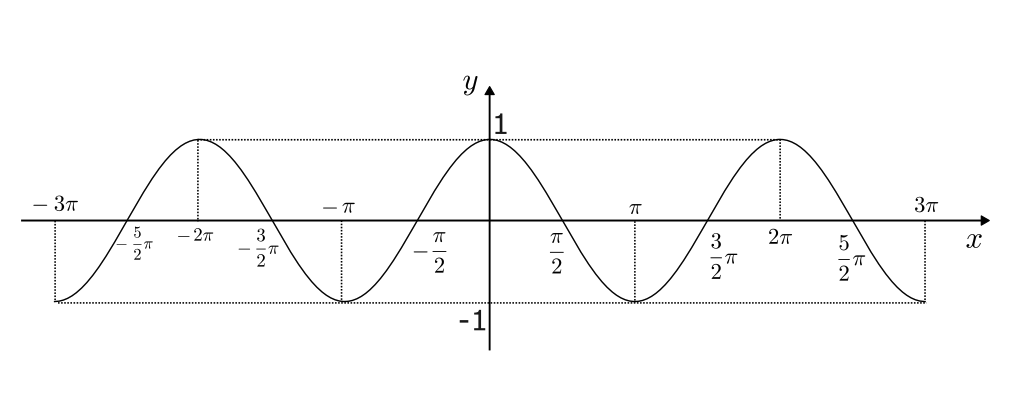
$x < 0$ や $x > 2\pi$ の場合も考えると、$y = \sin x$ は以下のようなグラフになる。
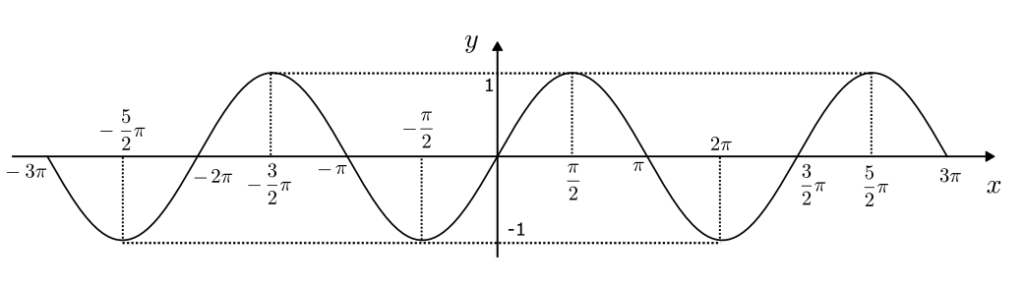
$y = \cos x$
$y = \cos x$ の場合も $y = \sin x$ と同様に考ていく。
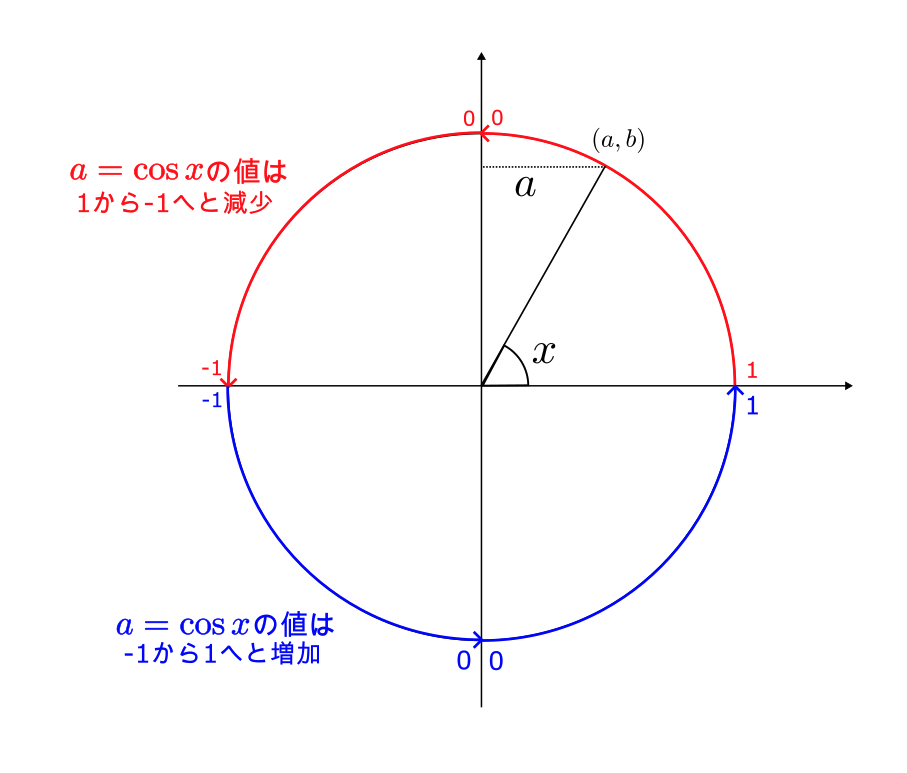
$\cos x$ の場合は $\cos x = a$ となる。
角度 $x$ が増加すると、$a$ の値は $0 < x < \pi$ では 1 から $-1$ に向かって減少し、$\pi < x < 2\pi$ では $-1$ から 1 に向かって増加する。
よって、$y = \cos x$ は以下のようなグラフになる。
$y = \tan x$
簡単に点を取ってみる
簡単に求められる範囲で、 $y=\tan x\ (0\leq x\leq 2\pi)$ の表は以下となる。
| $x$ | 0 | $\frac{\pi}{6}$ | $\frac{\pi}{4}$ | $\frac{\pi}{3}$ | $\frac{\pi}{2}$ |
|---|---|---|---|---|---|
| $y$ | 0 | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | / |
| $x$ | $\frac{2}{3}\pi$ | $\frac{3}{4}\pi$ | $\frac{5}{6}\pi$ | $\pi$ |
|---|---|---|---|---|
| $y$ | $-\sqrt{3}$ | $-1$ | $-\frac{1}{\sqrt{3}}$ | 0 |
| $x$ | $\frac{7}{6}\pi$ | $\frac{5}{4}\pi$ | $\frac{4}{3}\pi$ | $\frac{3}{2}\pi$ |
|---|---|---|---|---|
| $y$ | $\frac{1}{\sqrt{3}}$ | 1 | $\sqrt{3}$ | / |
| $x$ | $\frac{5}{3}\pi$ | $\frac{7}{4}\pi$ | $\frac{11}{6}\pi$ | $2\pi$ |
|---|---|---|---|---|
| $y$ | $-\sqrt{3}$ | $-1$ | $-\frac{1}{\sqrt{3}}$ | 0 |
上記の表の通りに点を取ってみると以下のような図になる。
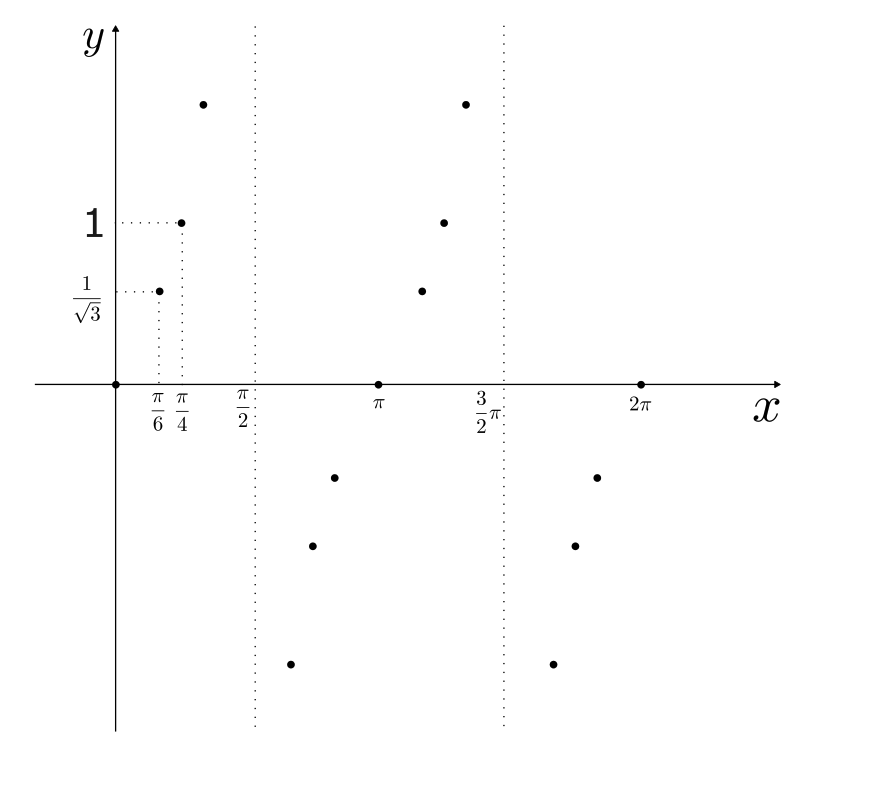
図を見てみると、$0 \leq x < \frac{\pi}{2}$ では増加、$\frac{\pi}{2} < x < \frac{3}{2}\pi$ では負の値から正の値に増加、$\frac{3}{2}\pi < x \leq 2\pi$ は負の値から0へ増加しているように見える。
もう少し詳しく見てみる
$0 \leq x < \frac{\pi}{2}$ の場合について見てみる。
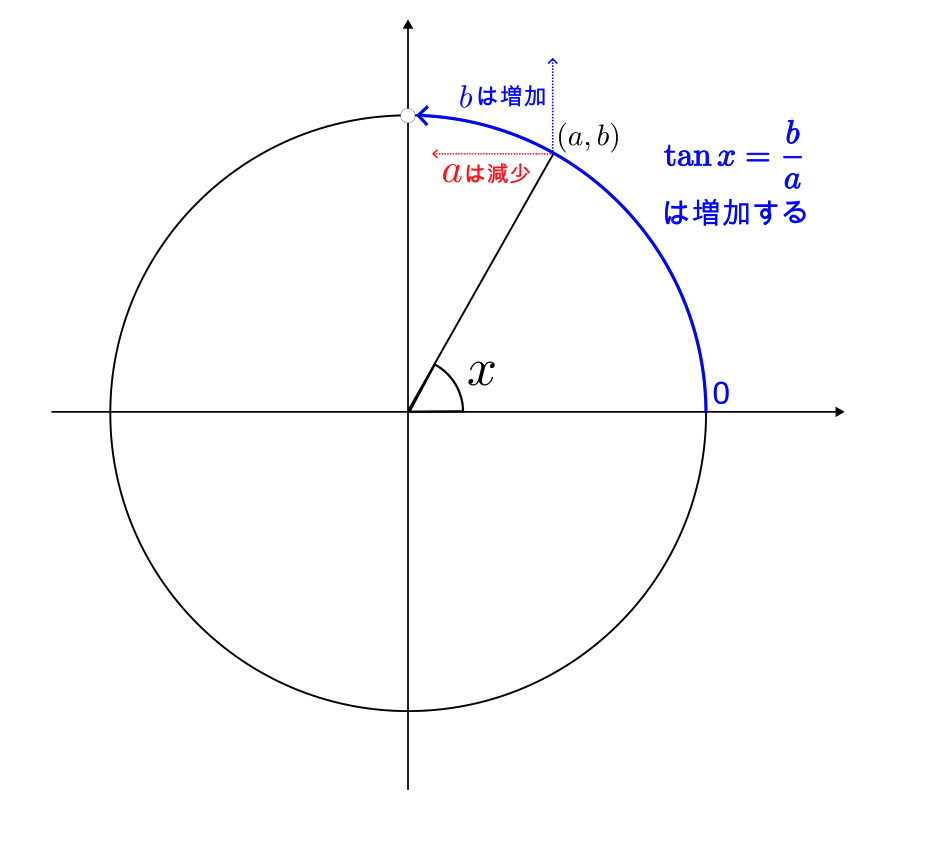
$x$ が増加すると、分母である $a$ は減少し、分子である $b$ は増加するため、$\tan x = \frac{b}{a}$ は増加する。
$0 \leq x < \frac{\pi}{2}$ では $\tan x$ は増加し続けるが、$x = \frac{\pi}{2}$ の場合は $\tan x$ は存在しない。
次に、$\frac{\pi}{2} < x \leq \pi$ の場合について見てみる。
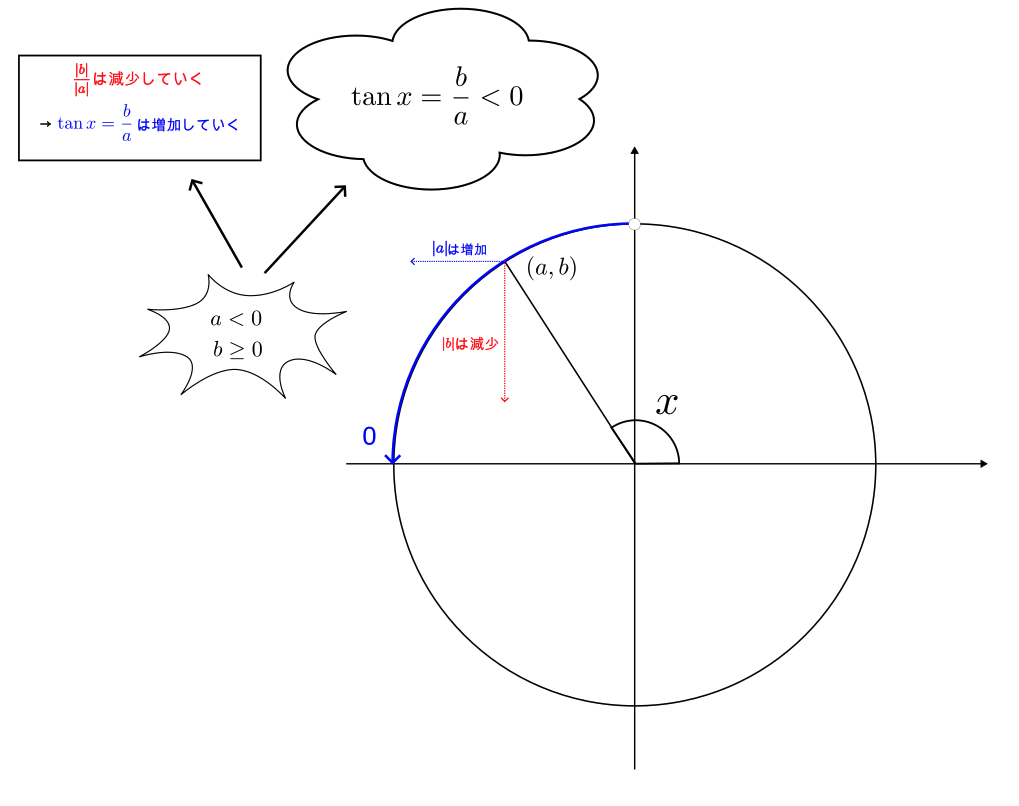
$a < 0$ であることに注意する。$x$ が増加すると、$|a|$ は増加し、$b$ は減少するため $\frac{b}{|a|}$ は減少する。よって、$x$ が増加すると、$\tan x = \frac{b}{a}$ は $\tan \pi = 0$ まで増加する。
$\pi \leq x < \frac{3}{2}\pi$ の場合は、$x$ が増加すると、$|a|$は減少し $|b|$ は増加するため、$\tan x = \frac{b}{a}$ は増加する。
$\tan \frac{3}{2}\pi$ は存在しない。
$\frac{3}{2}\pi < x \leq 2\pi$ の場合は、$\tan x = \frac{b}{a}$ は 0 まで増加する。
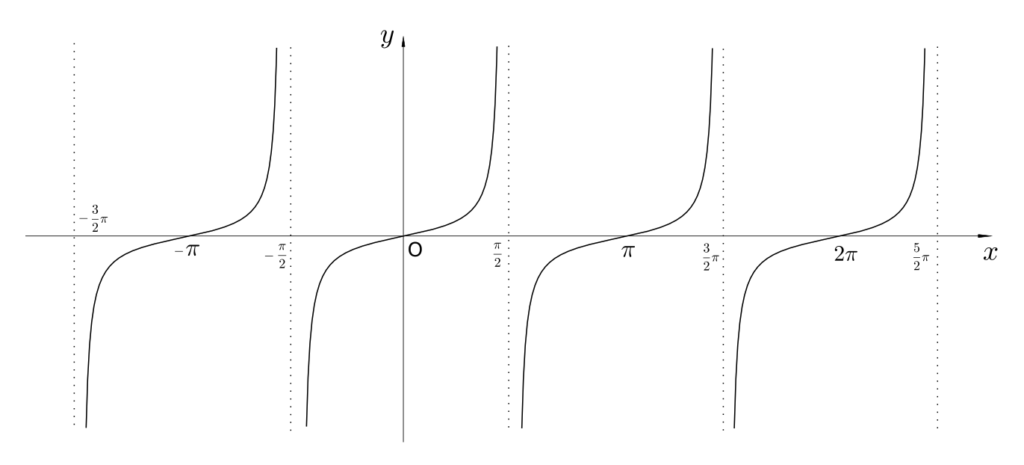
よって、$y = \tan x$ は以下のようなグラフになる。
周期関数
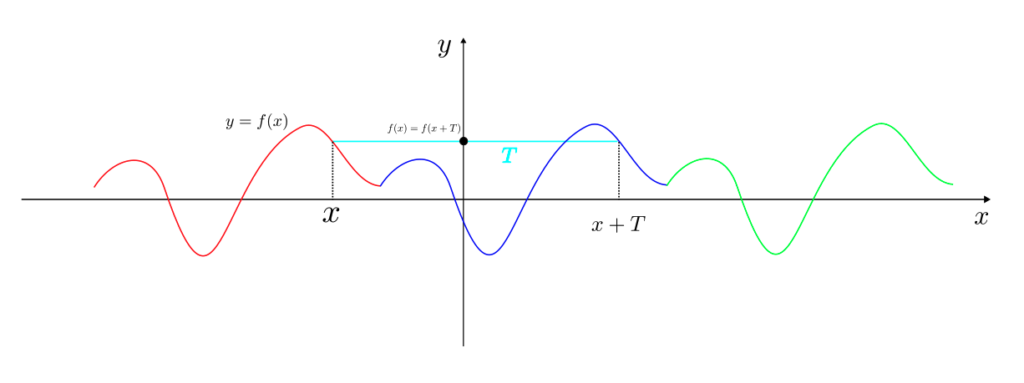
関数 $y = f(x)$ に対して、$f(x + T) = f(x)$ を満たす定数 $T\neq0$ が存在するとき、関数 $y = f(x)$ は周期関数という。
また、$f(x + T) = f(x)$ を満たす最小の $T > 0$ を周期という。
例
$y = \sin x$ と $y = \cos x$ は周期 $2\pi$ 、$y = \tan x$ は周期 $\pi$ の周期関数である。
Note
グラフの増加の仕方や減少の仕方にも種類があるが今回は気にしないことにする。


