事前知識
三角関数の相互関係
以下の関係式が成り立つ。
$$
\sin^2\theta + \cos^2\theta = 1 \label{1}\tag{1}
$$
$$
\tan\theta = \frac{\sin\theta}{\cos\theta} \label{2}\tag{2}
$$
$$
1 + \tan^2\theta = \frac{1}{\cos^2\theta} \label{3}\tag{3}
$$
$\sin^2\theta + \cos^2\theta = 1$
この等式は三平方の定理から成り立つことが分かる。
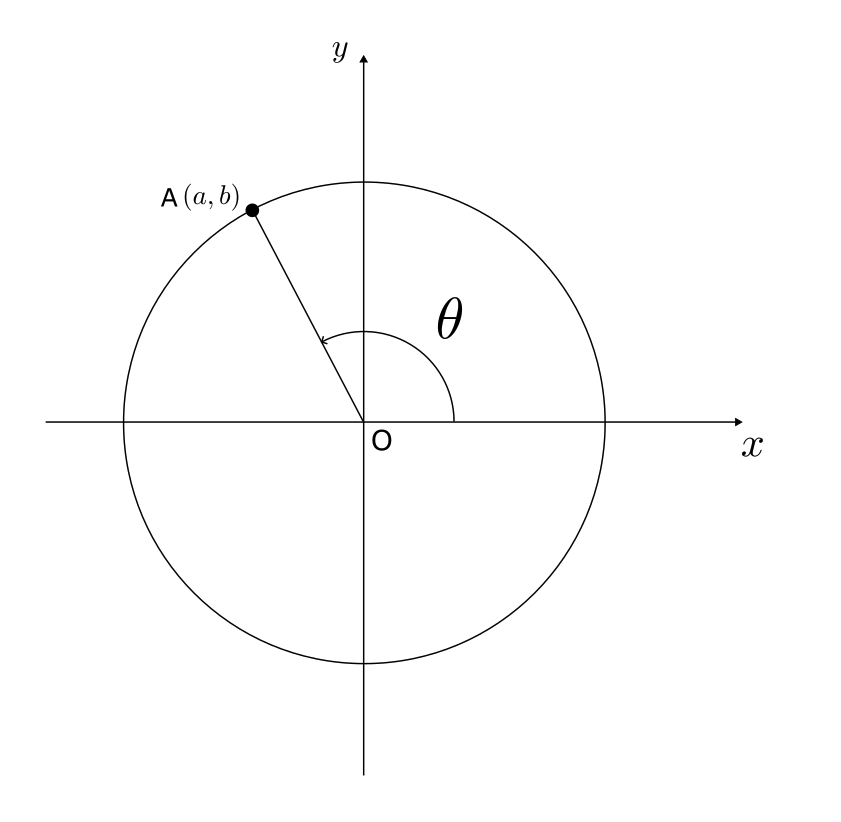
以下のような単位円を考え、角度 $\theta$ をとる。

図のように、点Aから $x$ 軸に垂線をおろしたときの $x$ 軸との交点をBとする。
このとき、三平方の定理より
$$
\begin{align}
OB^2 + BA^2 &= OA^2 \\
a^2 + b^2 &= 1
\end{align}
$$
が成り立つ。$a = \cos\theta,\ b = \sin\theta$ より
$$
\cos^2\theta + \sin^2\theta = 1
$$
となる。よって、$(\ref{1})$ が成り立つ。
$\tan\theta = \frac{\sin\theta}{\cos\theta}$
以下の図のような $\theta$ と点A$(a,b)$をとる。
$$
\sin\theta = b,\ \cos\theta = a,\ \tan\theta = \frac{b}{a}
$$
より、$(\ref{2})$ が成り立つことが分かる。
$ 1 + \tan^2\theta = \frac{1}{\cos^2\theta}$
$(\ref{1}),\ (\ref{2})$ から $\sin\theta$ を削除することにより、$(\ref{3})$ を導き出せる。
$$
\tan\theta = \frac{\sin\theta}{\cos\theta}
$$
より、
$$
\sin\theta = \tan\theta\cos\theta \tag{2′}\label{2′}
$$
となる。$(\ref{1})$ に $(\ref{2′})$ を代入すると、
$$
\begin{align}
\sin^2\theta + \cos^2\theta &= 1 \\
\tan^2\theta\cos^2\theta + \cos^2\theta &= 1 \\
(1 + \tan^2\theta)\cos^2\theta &= 1 \\
1 + \tan^2\theta &= \frac{1}{\cos^2\theta}
\end{align}
$$
となる。
例
三角関数の相互関係を利用することにより sin, cos, tan のどれか一つが分かっていれば残り2つの三角関数が求められる。
$\sin\theta = \frac{5}{13}$ とするとき、cos と tan を求める。
$$
\sin^2\theta + \cos^2\theta = 1
$$
より
$$
\begin{align}
\left(\frac{5}{13}\right)^2 + \cos^2\theta &= 1 \\
\cos^2\theta &= 1 – \left(\frac{5}{13}\right)^2 \\
\cos^2\theta &= \frac{144}{169}
\end{align}
$$
となるため、$\cos\theta$ は $\frac{12}{13}$ または $-\frac{12}{13}$ である。
( i ) $\cos\theta = \frac{12}{13}$ の場合
$$
\tan\theta = \frac{\sin\theta}{\cos\theta}
$$
より、
$$
\tan\theta = \frac{\frac{5}{13}}{\frac{12}{13}} = \frac{5}{12}
$$
( ii ) $\cos\theta = -\frac{12}{13}$ の場合
$$
\tan\theta = \frac{\frac{5}{13}}{-\frac{12}{13}} = -\frac{5}{12}
$$
よって、
$$
\cos\theta = \frac{12}{13},\ \tan\theta = \frac{5}{12}
$$
または
$$
\cos\theta = -\frac{12}{13},\ \tan\theta = -\frac{5}{12}
$$


