ベクトル

ベクトルとは

「大きさ」と「向き」を持つ量

記号

ベクトルを表す記号は $\vec{a}$ と書く。

点 A から 点 B までのベクトルを $\overrightarrow{\mathrm{AB}}$ と書く。

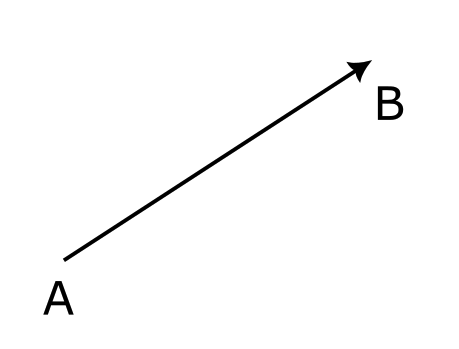
また、図のように矢印の始まりの点を「始点」、終わりの点「終点」と呼ぶ。
(図では A が始点、B が終点)

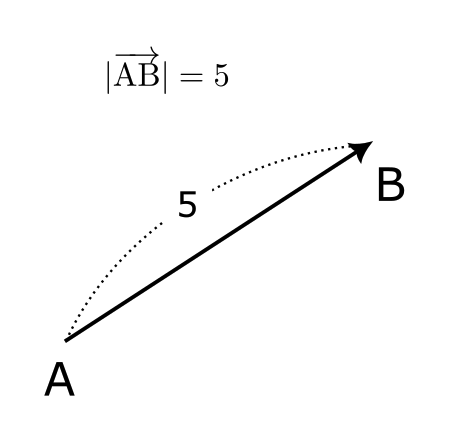
ベクトルの大きさを $|\vec{a}|$ や $|\overrightarrow{\mathrm{AB}}|$ ののように書く。

単位ベクトル

大きさが1のベクトルを単位ベクトルという。

ベクトルの足し算

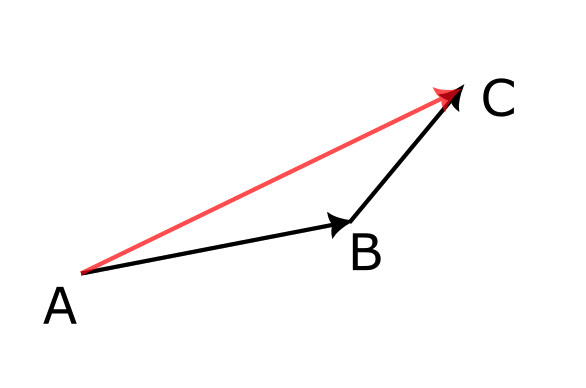
図のように $\overrightarrow{\mathrm{AB}}$ と $\overrightarrow{\mathrm{BC}}$ があるとき、$\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{BC}}$ は赤色のベクトル $\overrightarrow{\mathrm{AC}}$ である。

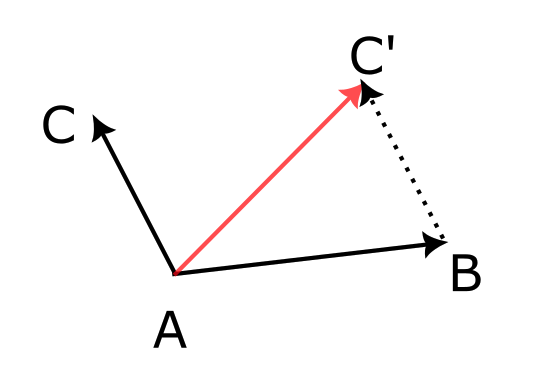
上の図のように足される方のベクトル ($\overrightarrow{\mathrm{AB}}$) の終点 と足す方のベクトル $\overrightarrow{\mathrm{AC}}$ の始点が一致していない場合でも、一方のベクトルを並行移動させることにより、ベクトルの和を表すことができる。
(図の場合、$\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{AC}}$ は始点が B になるところまで $\overrightarrow{\mathrm{AC}}$ を並行移動させる。並行移動させたベクトルの終点を C’としたとき、$\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{AC}} = \overrightarrow{\mathrm{AC’}}$ となる。)

逆ベクトル

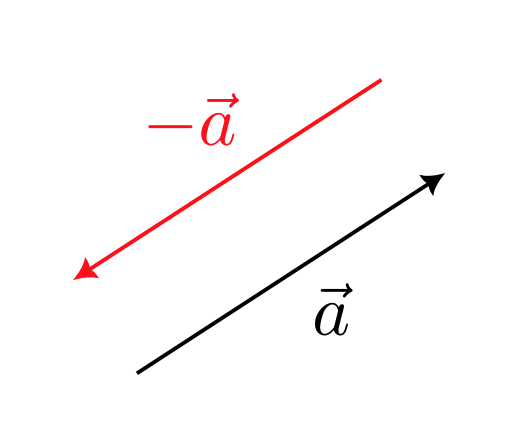
ベクトル $\vec{a}$ に対して、大きさが同じで向きが逆であるベクトルを逆ベクトルといい、$-\vec{a}$ と表す。

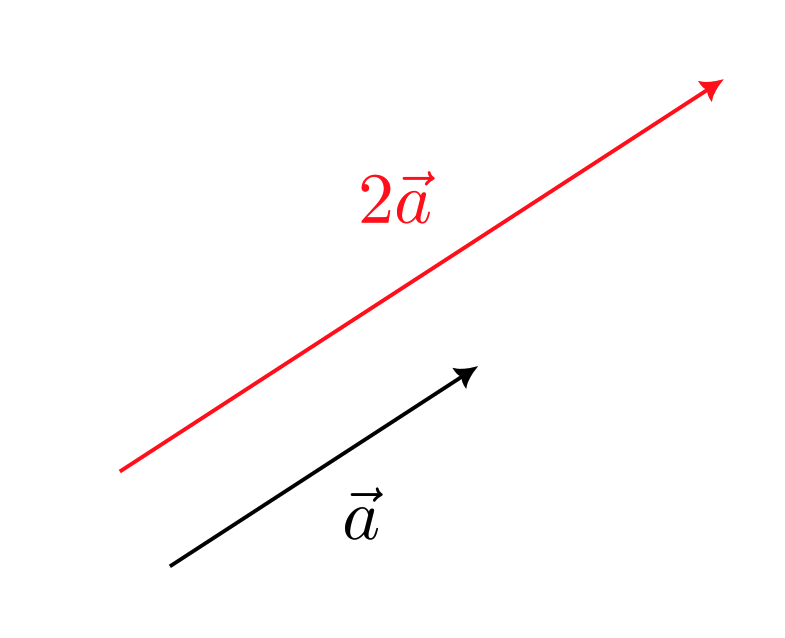
スカラー倍

$k$ を実数とする。$\vec{a}$ から大きさを $k$ 倍したベクトルを $k\vec{a}$ と書く。
$k\vec{a}$ を $k$ による $\vec{a}$ のスカラー倍と呼ぶ。